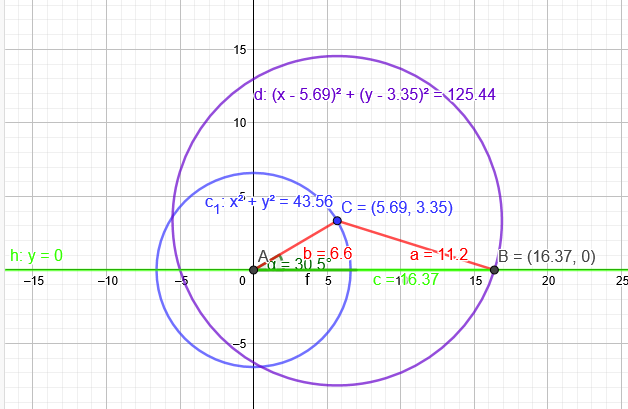
c) a = 11,2 cm; b = 6,6 cm; c= x (unbekannt) α= 30,5°
Gerade durch A(0|0) mit tan(35,5°):
f(x)=tan(35,5°)*x
Kreis um A(0|0) mit r=6,6
x^2+y^2=43,56
x^2+[tan(35,5°)*x]^2=43,56
x=5,69 (2. Lösung nicht nötig)
f(5,69 )=tan(35,5°)*5,69
C(5,69|3,35)
Kreis um C(5,69|3,35) mit r=11,2 schneidet x-Achse in B(16,37|0)
Somit ist c=16,37cm lang.
Nun lassen sich auch β und γ bestimmen, ebenso Sinus, Kosinus und Tangens der Winkel.