Berechne, wie viele Steine bestellt werden müssen.

Question

Aufgabe:

9. Einfahrten werden häufig mit Verbundsteinen gepflastert. Rechts siehst du die Maße eines Steines, der \( 7 \mathrm{~cm} \) hoch ist. Er wird aus Beton hergestellt; \( 1 \mathrm{~cm}^{3} \) Beton wiegt \( 2,5 \mathrm{~g} \).

a) Eine 30 m² große Einfahrt soll mit diesen Steinen gepflastert werden. Zur Sicherheit und wegen des Verschnittes werden \( 3 \% \) mehr Steine bestellt als mindestens nötig. Berechne, wie viele Steine bestellt werden müssen.

b) Ein gemieteter Kleinlaster hat eine Zuladung von \( 3 \mathrm{t} \). Wie viele Fahrten sind für den Transport der benötigten Steine erforderlich?

Problem/Ansatz:

Hallo es geht um no 9

habe so gemacht:

30m^2= 300000cm^2

1 Stein 16 * 20 = 320cm^2

300000 / 320 =937,5 Stein also 938 Stein

938 * 1,03 ( 3 % mehr) 966,14 Stein , also 967 Stein.

Stimmt bis hier erstmal? Wenn ja dann mache ich weiter , wenn nicht , dann bitte was falsch?

ich denke ich muss der Stein mit 20 * 16 ( ohne etwas abzuziehen)

Comments

Die obere Seite des Steins hat die Form eines Rechtecks, aus dem 2 Trapeze ausgeschnitten sind.

Berechne diese Fläche und multipliziere sie mit der Höhe=Dicke um das Volumen zu erhalten

Answer 1

Stimmt bis hier erstmal?

Nein, du hast ja den Stein so betrachtet, als sei die Grundfläche rechteckig.

Du musst noch die beiden Trapeze abziehen. Die Trapeze haben

parallele Seiten von 9cm und 14cm und die Trapezhöhe ist 3cm.

Also hat jedes die Fläche von 3*(14+9)/2  cm^2 = 34,5cm^2

Weil es 2 sind musst du für die Grundfläche des Steins rechnen

G = 320 cm^2 - 2*34,5cm^2 =251 cm^2

Und dann 300000cm^2:251cm^2 ≈1195,2  also 1196 Steine.

Dazu die 3% gibt dann 1232 Steine.

Comments

Das ist falsch, weil 2*3 ≠ 9  ist.

---

Das ist falsch, weil 2*3 ≠ 9  ist.

Ist vielleicht noch etwas früh, aber ich sehe keinen Fehler. Ich komme ebenso auf 1232 Steine.

---

Die Steinmaße sind nicht geeignet, die Ebene lückenlos zu parkettieren.

---

Die Steinmaße sind nicht geeignet, die Ebene lückenlos zu parkettieren.

Das ist zwar richtig. Wir müssen also den Rest der Steine nachher schön fein zermahlen und in die noch vorhandenen Lücken füllen.

Das sollte doch passen.

Auch rechteckige Steine von 16 cm x 20 cm wären evtl. nicht geeignet 30 m² zu pflastern ohne Steine zu zersägen. Das würde auf die genauen Maße der Fläche ankommen.

Ebenso müssen beim verlegen der Steine normal Fugen berücksichtigt werden. Auch das wurde bisher nicht gemacht.

Man könnte hier also nur an der Fragestellung Kritik üben.

---

Wir müssen also den Rest der Steine nachher schön fein zermahlen und in die noch vorhandenen Lücken füllen
Da wird man wohl Sand (extra zu bestellen) einfüllen.

Auch rechteckige Steine von 16 cm x 20 cm wären evtl. nicht geeignet 30 m² zu pflastern
Dafür sind doch extra die 3% einkalkuliert.

Ebenso müssen beim verlegen der Steine normal Fugen berücksichtigt werden. Auch das wurde bisher nicht gemacht.
Richtig, es wurde von EUCH nicht gemacht.

an der Fragestellung Kritik üben.
Soll das über eigene Unzulänglichkeiten hinweg täuschen ?
Ganz im Gegenteil, gerade weil Fugen vorgesehen werden müssen, ist die Fragestellung als realitätsnah lobend zu erwähnen.

Da in horizontaqler Richtung jedenfalls Fugen vorzusehen sind, kann man annehmen, dass diese auch in vertikaler Richtung eingeplant werden sollten. Ein Kompromiss zwischen Exaktheit und Einfachheit könnte demnach so

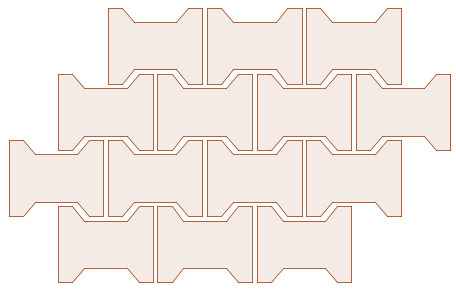
aussehen, bei der jeder Stein eine Fläche von 21cm x 14cm beansprucht.

---

Die Steinmaße sind nicht geeignet, die Ebene lückenlos zu parkettieren

Die Steine sind nicht dafür gedacht auf Stoß verlegt zu werden. Mit 1,5cm Fuge sind die aber sehr wohl zum pflastern geeignet.

Edit: Wie dein letztes Bild auch zeigt.

---

Hallo ,

Flüche von Stein

also  20 *16 - 2(14+9)/2 *3 = 251cm^2

300000/251= 1195 Stein → 1196 → 1196 *1.03=1231-->1232 Stein

Volumen des Steines 251 cm^2  * 7cm = 1757 cm^3

1757cm^3  * 1232 =2164624cm^3

Gewicht =2164624cm^2 * 2.5g/cm^3 = 5411560 g-->4,5 T unegefähr

also 5t /3t =1,8 Mal → also 2 Mal?

stimmt alles?

Text erkannt:

\( \begin{array}{lll}\text { 9. a) Fläche eines Steinestas } & 352 \mathrm{~cm}^{3} & 756 \mathrm{~cm}^{3} \\ & & \end{array} \)
zu pflastemde Fines: \( 251 \mathrm{~cm}^{2}=0,0251 \mathrm{~m}^{2} \)
ve): \( 30.9 \mathrm{~m}^{2} \)
? benŏtigte Steine: \( \frac{30.9 \mathrm{~m}^{2}}{0.0251 \mathrm{~m}^{2}} \approx 1231.08 \)
b) Volumen eines Steines: \( 251 \mathrm{~cm}^{2} \cdot 7 \mathrm{~cm}=1757 \mathrm{~cm}^{3}=1.757 \mathrm{dm}^{3} \)
Gewicht eines Steines: \( 1757 \mathrm{~cm}^{3}-\frac{2.5 \mathrm{~g}}{\mathrm{~cm}^{3}}=4392.5 \mathrm{~g} \)
Gewicht der benötigten Menge: \( 5411560 \mathrm{~g}=5411,56 \mathrm{~kg}=5,41156 \mathrm{t} \)
Der Lkw muss 2 -mal fahren.

---

Ja das stimmt. Aber warum fragst du, wenn du die Lösung aus dem Buch schon hast?

---

Vielleicht beschäftigt der FS gerne andere Leute.

---

Ich denke nicht, dass hier verlegetechnische Aspekte zu berücksichtigen sind

Viele Matheaufgaben aus dem Leben gehen an der Realität vorbei bzw.

berücksichtigen Details nicht. Deswegen ist hier nur vom Verschnitt die Rede.

---

Außer dem Gast hj... ist das hier jedem klar.

---

Ich denke nicht, dass hier verlegetechnische Aspekte zu berücksichtigen sind. Viele Matheaufgaben aus dem Leben gehen an der Realität vorbei bzw. berücksichtigen Details nicht. Deswegen ist hier nur vom Verschnitt die Rede.

Endlich jemand der kapiert hat wie Schulbücher aufgebaut sind und wie die Aufgaben zu verstehen sind.

Vielleicht ist auch jemandem schonmal aufgefallen, dass bei Wurfaufgaben in der Physik in Schulbüchern immer ohne den Luftwiderstand gerechnet wird.

Wenn man Verlegetechniken, Parkettierungen, Fugen und ähnliches berücksichtigen sollte, wäre darauf in Schulbüchern explizit nochmal eingegangen worden.

---

Nur weil Menschen die dumme Aufgaben stellen auch dumme Lösungen erwarten, heißt das nicht, dass man ihnen keine sinnvolleren Lösungen vorschlagen darf. Erkennt man nämlich das von hj angesprochene Problem und versucht es in einer Lösung zu berücksichtigen, so lernt man dabei schlussendlich wesentlich mehr, als wenn man die Aufgabe einfach stupide durchrechnet.

Einen Relaitätsbezug zu suggerieren und dann gleichzeitig so bekloppte Maße für die Steine zu wählen, dass der angedachte Lösungsweg gar keinen Sinn ergibt, ist die reinste Idiotie.

---

Das wäre eigentlich kein Problem, wenn Lehrer abweichende Lösungen anerkennen würden. Solange die Lehrer aber abweichende Lösungen mit falsch bewerten wird das Ganze zum Verhängnis.

---

also soll ich nicht die Lösung im Buch gucken, nach gemeinsam lösen? Ich gucke die Lösung erst später um zu sehen ob die Lösung im Buch falsch ist, damit ich diese Lösung markiere( falsch) damit ich nicht durcheinander bin.Weil ich zuerst OHNE Buch zuerst lernen möchte

---

Endlich jemand der kapiert hat wie Schulbücher aufgebaut sind und wie die Aufgaben zu verstehen sind.

Frei nach dem Motto: nicht für das Leben, sondern für die Schule lernen wir!??

Einen Relaitätsbezug zu suggerieren und dann gleichzeitig so bekloppte Maße für die Steine zu wählen, dass der angedachte Lösungsweg gar keinen Sinn ergibt, ist die reinste Idiotie.

dem kann ich nur zustimmen!

@Zahri:

also soll ich nicht die Lösung im Buch gucken, nach gemeinsam lösen?

Du hast ja hier nun schon mehr als eine Lösung präsentiert bekommen. Schau Dir  also auch die Lösung im Buch an und entscheide dann selber, welche von diesen Lösungen sinnvoll ist. Schreibe Deine Argumente zusammen und diskutiere sie mit Deiner Lehrerin oder Lehrer.

Dann machst Du alles richtig.

Noch ein Hinweis: diese Pflastersteine heißen Doppel-T-Pflastersteine oder H-Verbundsteine. Das Format ist 20x16,5cm (DT-200/165) und dieses Format enthält bereits die Fugenbreite von ca. 3mm. Das Nennmaß ist \(197\times 162\,\text{mm}\).

Der Flächenbedarf wird von den Lieferanten mit 35St/qm \((\to 286\,\text{cm}^2)\) angegeben, was IMHO etwas zu viel ist. Sie sind in Höhen von 6cm, 8cm und 10cm lieferbar.

---

Ich habe mich entschieden so zu machen. Geht das?
also 20 *16 - 2(14+9)/2 *3 = 251cm2

300000/251= 1195 Stein → 1196 → 1196 *1.03=1231-->1232 Stein

Volumen des Steines 251 cm2  * 7cm = 1757 cm3

1757cm3  * 1232 =2164624cm3

Gewicht =2164624cm2 * 2.5g/cm3 = 5411560 g-->4,5 T unegefähr

also 5t /3t =1,8 Mal → also 2 Mal?

stimmt?

---

Hallo Zahri,

Ich habe mich entschieden so zu machen. Geht das?

Ja - das geht und das stimmt auch so.