Aufgabe:
Guten Abend
ich bräuchte eine Erklärung für den zweiten, so wie dem vierten Schritt.
Warum steht beim zweiten Schritt auf einmal (4 + 6)?
Warum wird im vorletzten Schritt nicht halbiert, also n(n+1)/2?
Vielen Dank im Voraus! :)
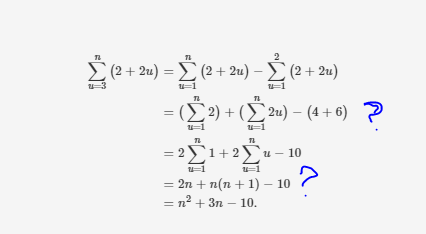
Text erkannt:
\( \begin{aligned} \sum \limits_{u=3}^{n}(2+2 u) &=\sum \limits_{u=1}^{n}(2+2 u)-\sum \limits_{u=1}^{2}(2+2 u) \\ &=\left(\sum \limits_{u=1}^{n} 2\right)+\left(\sum \limits_{u=1}^{n} 2 u\right)-(4+6) \\ &=2 \sum \limits_{u=1}^{n} 1+2 \sum \limits_{u=1}^{n} u-10 \\ &=2 n+n(n+1)-10 \\ &=n^{2}+3 n-10 \end{aligned} \)
Problem/Ansatz: