Aufgabe:
Ein Ackerbau wird mit x1 Einheiten Naturdünger und mit x2 Einheiten Kunstdünger behandelt. Die Ertragsfunktion lautet:
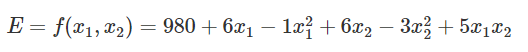
Text erkannt:
\( E=f\left(x_{1}, x_{2}\right)=980+6 x_{1}-1 x_{1}^{2}+6 x_{2}-3 x_{2}^{2}+5 x_{1} x_{2} \)
Der Düngemitteleinsatz von derzeit 7 Einheiten Naturdünger und 15 Einheiten Kunstdünger wird geändert, so dass 3% weniger Naturdünger und 1.7% mehr Kunstdünger eingesetzt werden.
a. Approximieren Sie die Änderung des Ertrags mit Hilfe des totalen Differentials.
b. Wie hoch ist die exakte Veränderung des Ertrags?
Problem/Ansatz:
Guten Abend!!
Bei meinem Rechenweg muss ein Fehler drinn sein.
a) Habe die Partielle Ableitung von x1 und x2 berechnet, die werte 7 für x1 und 15 für x2 eingetragen und Ergebnisse addiert. Als Ergebnis habe ich 18 bekommen.
b) Bei b habe ich die abgewandten WErte (also statt 7 6,79 und statt 15 15,255 genommen).
Könnte mir vielleicht jemand verraten wo mein Rechenfehler liegt? Mir scheint mein Rechenweg nicht ganz korrekt. Trotz ähnlicher Aufgaben hier auf der Mathelounge habe ich ein falsches Ergebnis. Wäre sehr dankbar!