Additionstheoreme für Winkelfunktionen

Question

Derhmatrix Dα ∈ M_2,2 (ℝ)

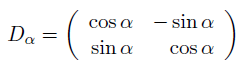
Text erkannt:

$D_{\alpha}=\left(\begin{array}{rr}\cos \alpha & -\sin \alpha \\ \sin \alpha & \cos \alpha\end{array}\right)$

ich soll zeigen, dass für α,β ∈ ℝ die Gleichung :

Text erkannt:

$D_{\alpha} D_{\beta}=D_{\alpha+\beta}=D_{\beta} D_{\alpha}$

erfüllt ist.

Als Hinweis habe ich, dass ich die Additionstheoreme für die Winkelfunktionen verwenden soll.

ich hab alpha ausgeklammert, hat mir aber nichts gebracht, wie holen die da beta dazu?

Answer 1

Rechne das Produkt aus D_α*D_ß da steht z.B. obne links

cos α * cos ß - sin α * sin ß

und bei der Matrix für D_a+ß steht dort cos(a+ß)

und nach dem Add.theorem für cos ist das

beides gleich.

Comments

das verstehe ich nicht ganz , tut mir leid

---

Rechne mal das Matrizenprodukt

$\left(\begin{array}{rr}\cos \alpha & -\sin \alpha \\ \sin \alpha & \cos \alpha\end{array}\right) \cdot \left(\begin{array}{rr}\cos \beta & -\sin \beta \\ \sin \beta & \cos \beta\end{array}\right)$

aus und schreib was du raus hast.

---

Additionstheoreme sind Formeln z.B. für cos(a+ß) und sin(a+ß).

Frage Tante Google oder Wikipedia oder deine Formelsammlung.

---

cos α * cos β + (-sin α * sin β)

und

sin α * (-sin β) + cos α * cos β

---

Die Produktmatrix hat doch 4 Elemente.

cos α * cosβ β -sin α * sin ß               -cos α * sin β-sin α * cos β
sin α * cosβ β +cos α * sin ß             sin α * (-sin β) + cos α * cos β

und das vergleiche mit den Add.theoremen.