Aufgabe:
Aufgabe:
Distanzen spielen in der Graphentheorie eine sehr große Rolle. In dieser Aufgabe wollen wir einen Algorithmus entwerfen, der den Durchmesser eines Graphen bestimmt, d.h. die maximale kürzeste Distanz zwischen zwei Knoten. Dazu definieren wir folgendes.
• Die Distanz dist(v, w) zwischen zwei Knoten v, w ∈ V im einem Graphen G ist die Anzahl an Kanten auf einem kürzesten Weg zwischen v und w in G. Gibt es keinen Weg zwischen v und w, so ist dist (v, w) = ∞.
• Die Erzentrizität ex(v) eines Knotens v E V bezeichnet die Länge eines kürzesten Pfades zu dem am weitesten entfernten Knoten, d.h. ex(v) := maxw∈v (dist (v, w).
• Der Durchnesser eines Graphen G entspricht dem Maximum über die Exzentrizitäten, d.h. diam(G):= maxv∈V (ex(v)).
Betrachte den in Abbildung 1 abgebildeten Graphen H. Gib folgende Punkte an:
(i) ex(v1) und ex(v2).
(ii) diam(H)
(iii) Menge V' ⊆ V an Knoten, sodass ex(w) = diam(H) für jeden Knoten w ∈ V' gilt.
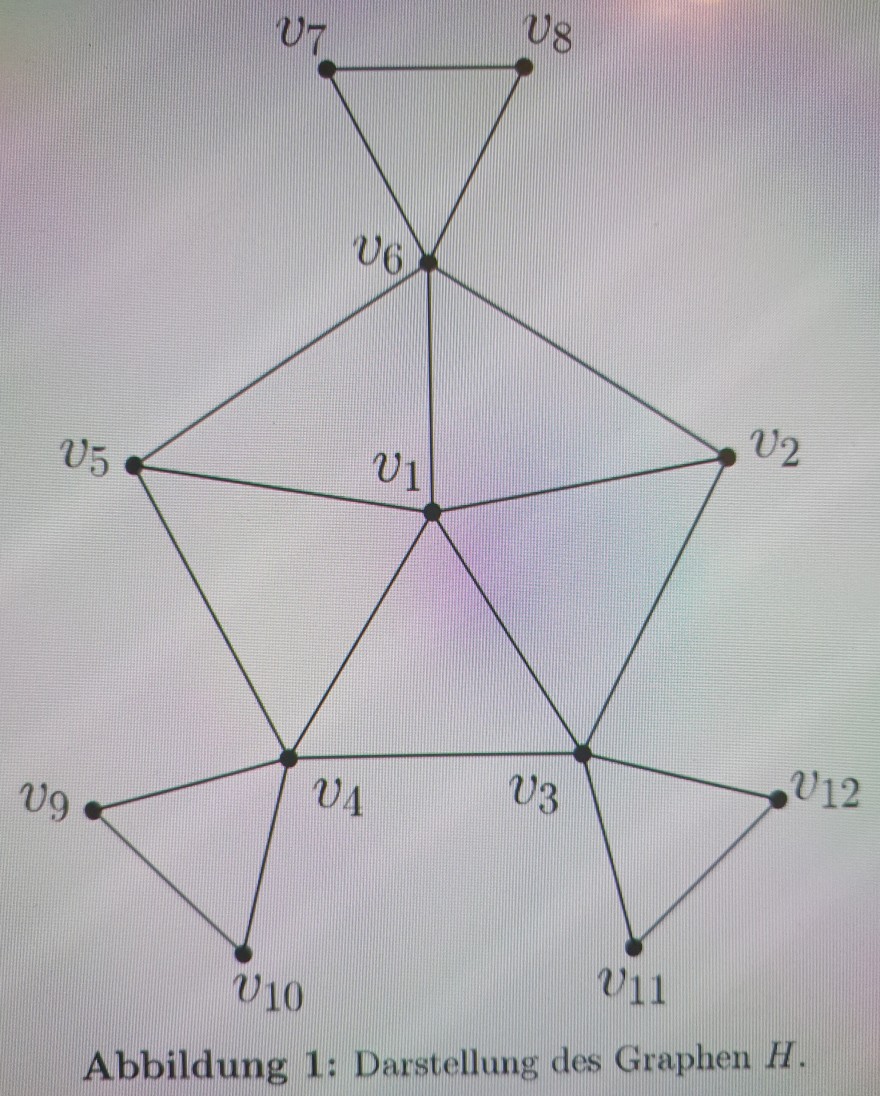
Text erkannt:
Abbildung 1: Darstellung des Graphen \( H \).
Problem/Ansatz:
Ich bin mir nicht ganz sicher, aber ich glaube bei (i) ist die folgende Lösung richtig und bei (ii) und (iii) habe ich keine Ahnung und ich hoffe, dass mir jemand hilft.
(i) ex(v1) = 2
ex(v2) = 3
(ii) ???
(iii) ???
Ich bitte um Ihre Hilfe.