Berechnen sie die fehlenden Größen des Dreiecks

Question

Aufgabe: Berechnen sie die fehlenden Größen des Dreiecks. (Erstellen sie unbedingt zu jeder Aufgabe eine Skizze, in der die gegebenen Größen schwarz und die gesuchten Größen rot eingetragen werden.)

                a)             b)            c)

a         |     ---      | 9,2 cm | 8,2 cm  |

b         |    ---      | 4 cm  |     --     |

c          | 7,7 cm  |  ---   | 11,7 cm |

alpha   | 114°       | 120°  |  ---       |

beta     | 35°        |  ---    |  ---       |

gamma | -            |  ---    | 100°      |

So, ich hoffe mal dass die Tabelle erkennbar und halbwegs übersichtlich ist und sich nicht verschiebt.

Problem/Ansatz:

Ich versuche diese Aufgabe nun schon länger zu lösen. Ich habe schon viel nachgelesen und auch Videos geschaut aber es geht nicht in meinen Kopf. Ich verstehe nicht wie ich bei a) a und b berechnen soll. Auch bei b) komme ich nicht weiter. Kann mir jemand auf die Sprünge helfen, wie ich das am Besten lösen kann?

Liebe Grüße, Temy

Answer 1

Ich vermute das sind alles Aufgaben zum Sinussatz. Warum versuchst du es also nicht mal damit.

a)

gamma = 180° - alpha - beta = 31°
a = c·sin(alpha)/sin(gamma) = 13,66
b = sqrt(a² + c² - 2·a·c·cos(beta)) = 8,575

b)

beta = asin(sin(alpha)·b/a = 22,12°
gamma = 180° - alpha - beta = 37,88°
c = sqrt(a² + b² - 2·a·b·cos(gamma) = 6,523

c)

Mal selber probieren?

b = 7,042
alpha = 43,65°
beta = 36,35°

Answer 2

Hallo,

zu a)

Gamma ist leicht auszurechnen.

Wende dann den Sinussatz an: \(\frac{a}{sin(\alpha)}=\frac{b}{sin(\beta)}=\frac{c}{sin(\gamma)}\)

Gruß, Silvia

Answer 3

Geradengleichung durch A und C

y=tan(114°)*x

Geradengleichung durch B und C

tan(180°-35°)=tan(145°)

\( \frac{y-0}{x-7,7} \)=tan(145°)

y=tan(145°)*x-tan(145°)*7,7

y=-0,7x+0,7*7,7=-0,7x+5,39

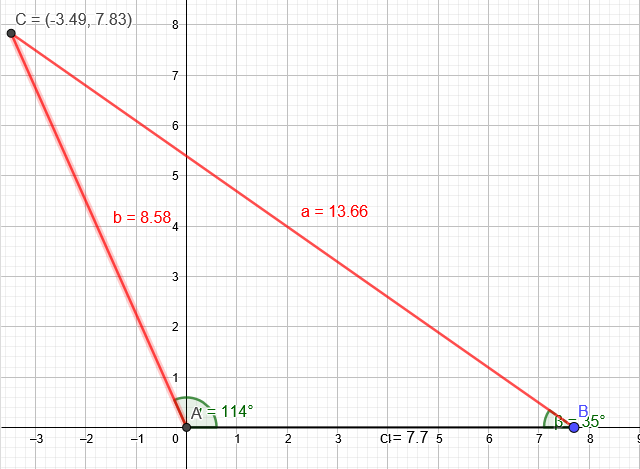
Beide Geraden schneiden sich in C(-3,49|7,83)

Mit dem Satz des Pythagoras kannst du nun b ausrechnen.

Analog die Berechnung von a.

Der Winkel γ ist leicht zu berechnen, da α und β gegeben sind.