Hallo,
Willkommen in der Mathelounge!
Es bietet sich grundsätzlich an, so etwas mit homogenen Koordinaten zu machen. Weiter benötigt man eine Matrix, die einen Punkt in ein System transformiert, dessen Z-Achse die Drehachse ist. Fest liegt$$\vec a = \begin{pmatrix}1/\sqrt 3\\ 1/\sqrt 3\\ 1/\sqrt 3\end{pmatrix}, \quad \vec p = \begin{pmatrix}1\\ 2\\ 3\end{pmatrix}$$
Dann brauchen wir einen Einheitsvektor der senkrecht auf \(\vec a\) steht, z.B.$$\vec n = \begin{pmatrix}1/\sqrt 2\\ -1/\sqrt 2\\ 0\end{pmatrix}$$Und der dritte Einheitsvektor berechnet sich aus dem Kreuzprodukt \(\vec o = \vec a \times \vec n\). Damit haben wir das System \({}^0T_D\) der Drehachse fertig:$${}^0T_D = \begin{pmatrix}\vec n& \vec o& \vec a& \vec p \\ 0& 0& 0& 1\end{pmatrix} \approx \begin{pmatrix}0.70711& 0.40825& 0.57735& 1\\ -0.70711& 0.40825& 0.57735& 2\\ 0& -0.81650& 0.57735& 3\\ 0& 0& 0& 1\end{pmatrix}$$Jetzt brauchen wir noch eine Transformation für die Drehung um die lokale Z-Achse. Dies ist allgemein:$${}^{\varphi}T_D = \begin{pmatrix}\cos(\varphi)& \sin(\varphi)& 0& 0\\ \sin(\varphi)& \cos(\varphi)& 0& 0\\ 0& 0& 1& 0\\ 0& 0& 0& 1\end{pmatrix}$$und für \(\varphi=60°\) ist \(\cos(\varphi) = 1/2\) und \(\sin(\varphi) = \sqrt 3/2\).
Und die Gesamttransformation \({}^{60°}T_0\) bsteht nun darin, einen Punkt in das "Drehsystem" \(D\) zu transformieren, dort zu drehen und wieder zurück in das Ausgangssystem \(0\) zu transformieren. Lese dazu die folgende Matrizenmultiplikation von rechts nach links.$${}^{60°}T_0 = {}^0T_D\cdot {}^{60°}T_{D} \cdot \underbrace{{}^DT_0}_{=\left({}^0T_D\right)^{-1}} = \begin{pmatrix}2/3& -1/3& 2/3& -1\\ 2/3& 2/3& -1/3& 1\\ -1/3& 2/3& 2/3& 0\\ 0& 0& 0& 1\end{pmatrix}$$
Als Beispiel ein Dreieck, welches ich um 60° gedreht habe. Die Drehachse ist die mangentafarbende Gerade.
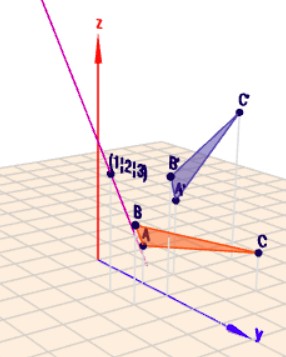
um das richtig zu sehen, musst Du auf das Bild klicken. Dann öffnet sich Geoknecht3D und Du kannst die Szene mit der Maus rotieren.
Du hast bestimmt noch Fragen. Melde Dich einfach.
Gruß Werner