ich habe Folgendes in der Literatur:
wir haben ein differenzierbares Vektorfeld F: X→ℝn mit X⊂ℝn
Einen Diffeomorphismus a: X → Y
Wir interessieren uns für die Transformation von Integralkurven.
Für Lösungskurven von f(t) setzen wir f'(t) = F(f(t)) und g(t) = a(f(t))
Wir erhalten G(g(t)) = g'(t) = a'(f(t))F(f(t)). G ist das transformierte Vektorfeld G
(a'(f(t)) ist hier dann die Jacobi-Matrix)
G: Y → ℝn , y = a(x) ↦ a'(x) * F(x)
Eine Eigenschaft ist, dass Equilibrien in Equilibrien transformiert werden, also F(x) = 0 ⇔ G(a(x)) = 0
Konkret habe ich nun dieses Beispiel:
Wir haben das Vektorfeld F: (x_1, x_2) ↦ (x_2+2x_1*x_2+2(x_2)^3, -x_1 - (x_2)^2)
und die Abbildung den Diffeomorphismus a: (x_1,x_2) ↦ (x_1 + (x_2)^2,x_2)
nun erhält man G(y_1,y_2) = \( \begin{pmatrix} 1 & 2x_2 \\ 0 & 1 \end{pmatrix} \) * \( \begin{pmatrix} x_2+2x_1*x_y+2(x_2)^3\\-x_1 - (x_2)^2 \end{pmatrix} \) = \( \begin{pmatrix} x_2\\-x_1-(x_2)^2 \end{pmatrix} \)
Die Lösung g in den transformierten Koordinaten, also von g'(t) = G(g(t)) soll nun sein:
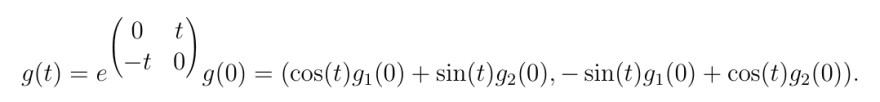
Text erkannt:
\( g(t)=e^{\left(\begin{array}{cc}0 & t \\ -t & 0\end{array}\right)} g(0)=\left(\cos (t) g_{1}(0)+\sin (t) g_{2}(0),-\sin (t) g_{1}(0)+\cos (t) g_{2}(0)\right) \)
Wie kommt man auf die Lösung im letzten Schritt (also g(t))?