Abstand zweier paralleler Geraden bestimmen

Question

Aufgabe:

Wie könnte der Abstand der beiden parallelen Geraden g : x − 2y = 4 und
h : y = 1/2*x + 1 voneinander bestimmt werden? Wie groß ist dieser Abstand?

Ist der Weg über die Hessesche Normalenform der einfachste oder könnte man die Werte auch in eine bestimmte Formel einsetzen?

Comments

Dein h(x) ist unklar.

Du kannst den Abstand über eine Senkrechte, die beide Geraden schneidet, bestimmen,

indem du den Abstand der Schnittpunkte ermittelst.

Answer 1

Ist der Weg über die Hessesche Normalenform der einfachste

Definitiv ja

Der (gerichtete) Abstand eines Punktes (x | y) von g ist definiert nach Hesse als

d = (x - 2·y - 4)/√(1^2 + 2^2)

Setze hier einen Punkt der Geraden h ein, z.B. (0 | 1)

d = (0 - 2·1 - 4)/√(1^2 + 2^2) = - 6/5·√5 = -2.683

Beachte hierbei, dass d der gerichtete Abstand ist. Als Abstand kannst du hier dann einfach den Betrag nehmen.

Comments

Denk an die alten Römer: Variatio delectat, ab und zu! :)

Answer 2

Es gibt verschiedene Verfahren für die Abstandsbestimmung paralleler Geraden, eines ist so gut wie das andere.

Wenn du "Hesse" kannst, dann nimm einfach "Hesse".

Möglicherweise ist für andere Leute etwas anderes einfacher. Wenn du aber danach fragen musst, frisst die dafür notwendige Einarbeitung einen eventuellen Vorteil wieder auf.

Answer 3

Hallo,

senkrecht zu beiden Geraden verlaufen die Geraden mit y=-2x+b.

Mit b=1 also y=-2x+1.

Der Schnittpunkt mit h ist A(0|1).

Der Schnittpunkt mit g:

x-2(-2x+1)=4

5x=6

x=1,2

y=-2*1,2+1=-1,4

B(1,2|-1,4)

Der Abstand d der Geraden ist der Abstand der Punkte A und B.

Damit ist d=√(1,2^2+2,4^2)=6/5 *√5

:-)

Comments

Wie bist du auf die Gerade y=-2x+b gekommen? Könnte man zum Beispiel auch y=6x+y schreiben, weil (6,1) in g eingesetzt ja 0 ergibt, also senkrecht ist.

---

Die parallelen Geraden haben die Steigung 1/2. Orthogonale Geraden dazu haben die Steigung -2, da (-2)*(1/2)=-1 ist.

m1*m2=-1 ist die Bedingung für orthogonale Geraden.

Answer 4

g :
x − 2y = 4
2y = x - 4
g : y = 1/2*x - 2
h : y = 1/2*x + 1

Da die Steigung gleich ist sind es Parallelen

Skizze

m = tan((alpha) = 1/2
alpha = 26.57 °
beta = 90 - 26.57 = 63.43 °

Hypotenuse = 3
sin ( 63.43 ) = a (bstand) / 3
abstand = 2.68

Answer 5

Ich nehme den Punkt (4, 0) auf g und minimiere den Abstand zu einem Punkt auf der Parallelen h:

min. \( \sqrt{(x-4)^{2}+\left(\frac{1}{2} x+1-0\right)^{2}} = \frac{6}{\sqrt{5}} \)

Answer 6

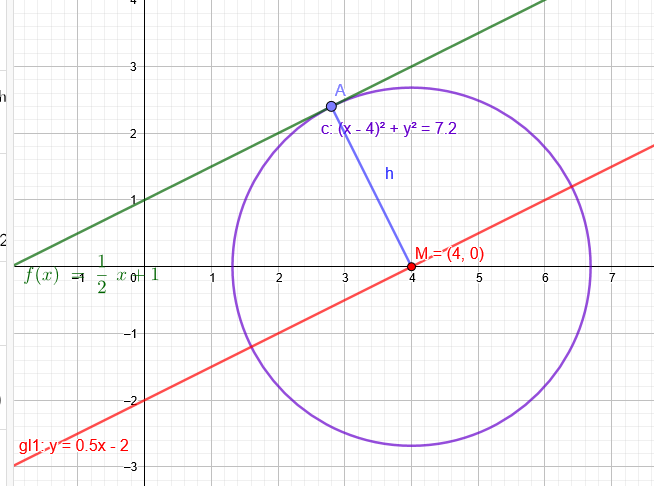
Wie könnte der Abstand der beiden parallelen Geraden g : x − 2y = 4 und
h : y = 1/2*x + 1 voneinander bestimmt werden? Wie groß ist dieser Abstand?

Kreis um M(4|0): (x-4)^2+y^2=r^2

y=0,5x+1 schneidet Kreis:

(x-4)^2+(0,5x+1)^2=r^2

x^2-8x+16+0,25x^2+x+1=r^2

\( \frac{5}{4} \)x^2-7x=r^2-17|*\( \frac{4}{5} \)

x^2-\( \frac{28}{5} \)x=\( \frac{4}{5} \)r^2-\( \frac{68}{5} \)

(x-\( \frac{14}{5} \))^2=\( \frac{4}{5} \)r^2-\( \frac{68}{5} \)+\( \frac{196}{25} \)=\( \frac{4}{5} \)r^2-\( \frac{144}{25} \)   | \( \sqrt{} \)

Tangente liegt vor, wenn \( \frac{4}{5} \)r^2-\( \frac{144}{25} \)=0

r=\( \frac{6}{5} \)*\( \sqrt{5} \) Das ist nun der Abstand der Parallelen.