Streckenzug der Koordinaten berechnen

Question

Aufgabe:

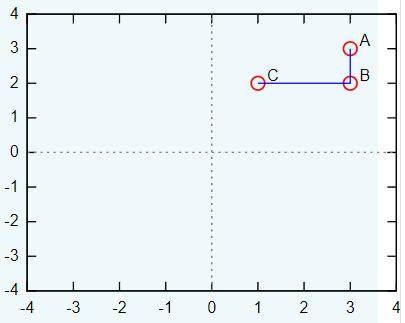
Gegeben sind drei Punkte A(3|3), B(3|2) und C(1|2). Die Grafik verbindet A, B und C zu einem L (Streckenzug).

Der Streckenzug wird durch die Matrix

A = (11)

    (01)

transformiert.
Geben Sie die neuen Koordinaten von L' an:

A' =

B' =

C' =

Problem/Ansatz:

Kann mir jemand bitte die Lösung oder den Lösungsweg zeigen?

Answer 1

Hallo,

Willkommen in der Mathelounge!

Bei dieser Transformation handelt es sich um eine Matrix-Vektor-Multiplikation. Es ist$$A'=\begin{pmatrix}1& 1\\ 0& 1\end{pmatrix} \cdot \begin{pmatrix}3\\ 3\end{pmatrix}= \begin{pmatrix}1\cdot3+1\cdot3\\ 0\cdot3+1\cdot 3\end{pmatrix}= \begin{pmatrix}6\\ 3\end{pmatrix}\\B'= \begin{pmatrix}1& 1\\ 0& 1\end{pmatrix}\cdot \begin{pmatrix}3\\ 2\end{pmatrix}=\begin{pmatrix}1\cdot3+1\cdot2\\ 0\cdot3+1\cdot 2\end{pmatrix}=\begin{pmatrix}5\\ 2\end{pmatrix}\\C'=\begin{pmatrix}1& 1\\ 0& 1\end{pmatrix}\cdot\begin{pmatrix}1\\ 2\end{pmatrix}=\begin{pmatrix}1\cdot1+1\cdot2\\ 0\cdot1+1\cdot 2\end{pmatrix}=\begin{pmatrix}3\\ 2\end{pmatrix} $$In der Ebene sieht das so aus:

Das grüne Punktetripel wird auf das blaue abgebildet. Die Matrix realisiert eine Scherung.

Gruß Werner