Substitution: Wo ist der Fehler?

Question

Aufgabe: substitution

Problem/Ansatz: Hallo, ich lerne grade wie man die nullstellen einer ganzrationalen Funktion mithilfe der substitution löst. Ich stecke grade an einer Aufgabe fest und weiß zwar, dass ich einen Fehler gemacht habe, aber nicht wo. Deswegen wollte ich hier nach Hilfe fragen.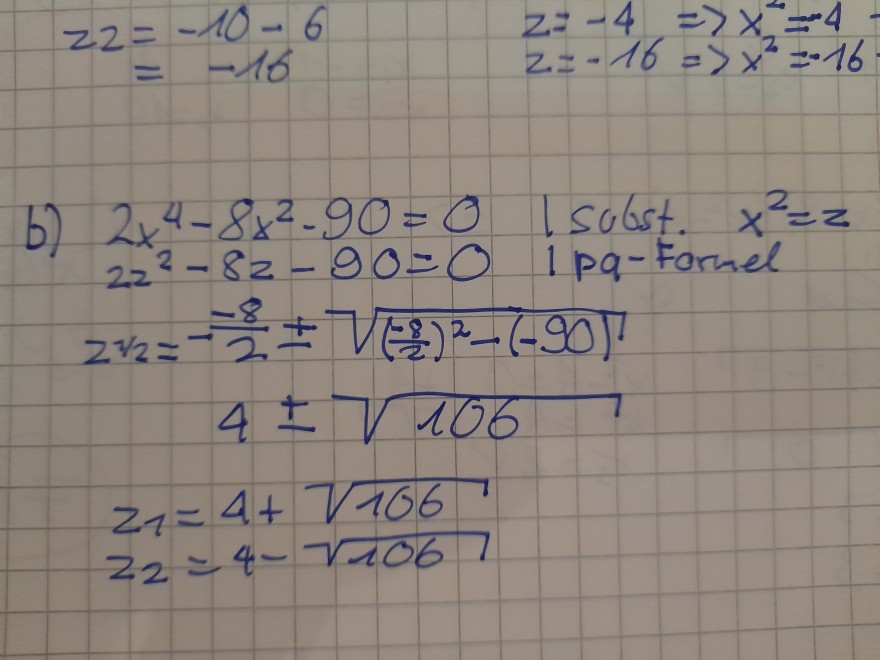

Text erkannt:

\( \begin{aligned} z 2 &=-10-6 & & z z-4 & \Rightarrow x^{2} &=4 \\ &=-16 & & z=-16 & \Rightarrow x^{2} &=-16 \end{aligned} \)
b) \( \begin{aligned} 2 x^{4}-8 x^{2}-90 &=0 \\ 2 z^{2}-8 z-90 &=0 \quad \text { isulist. } x^{2}=z \end{aligned} \)
\( 2 \sqrt{2}=-\frac{-8}{2} \pm \sqrt{\left(\frac{-8}{2}\right)^{2}-(-90)} \)
\( 4 \pm \sqrt{106} \)
\( z_{1}=4+\sqrt{106} \)
\( 2_{2}=4-\sqrt{106} \)

Answer 1

Hallo,

\(2z^2-8z-90=0\)

Die pq-Formel kannst du erst anwenden, wenn z alleine steht, also erst einmal alles durch 2 teilen:

\(z^2-4z-45=0\)

Jetzt kannst du die Fomel anwenden.

Gruß, Silvia

Comments

Omg stimmt, vielen Dank!!

Answer 2

Weg ohne Substitution:     mit quadratischer Ergänzung:

2x^4-8x^2-90=0 |:2

x^4-4x^2-45=0 |+45

x^4-4x^2=45

(x^2-\( \frac{4}{2} \))^2=45+(\( \frac{4}{2} \))^2=49  |\( \sqrt{} \)

1.)x^2-2=7

x^2=9 |  \( \sqrt{} \)

x₁=3

x₂=-3   Diese beiden Lösungen liegen in  ℝ .

2.)x^2-2=-7

x^2=-5=5i^2

x₃=i*\( \sqrt{5} \)

x₄=-i*\( \sqrt{5} \) Diese beiden Lösungen liegen in ℂ.