Question

Eine nach unten geöffnete Normalparabel schneidet die x-Achse bei x1 = -2 und bei x2 = -4                                           
a) Ermittle die Funktionsgleichung der Parabel, deren Scheitelpunktform und                                                                 
b) die Gleichung der Verbindungsgeraden vom Scheitelpunkt der Parabel zum Koordinatenursprung.

Answer 1

 

Parabel: f(x) = ax² + bx + c

Normalparabel: f(x) = x² + bx + c

Normalparabel nach unten geöffnet: f(x) = -x² + bx + c

Wir setzen ein:

I. f(-2) = - 4 - 2b + c = 0

II. f(-4) = -16 - 4b + c = 0

 

II. - I.

-12 - 2b = 0

b = - 6

Das in I. eingesetzt:

- 4 + 12 + c = 0

c = - 8

Die Gleichung der Funktion lautet also:

f(x) = - x² - 6x - 8

 

 

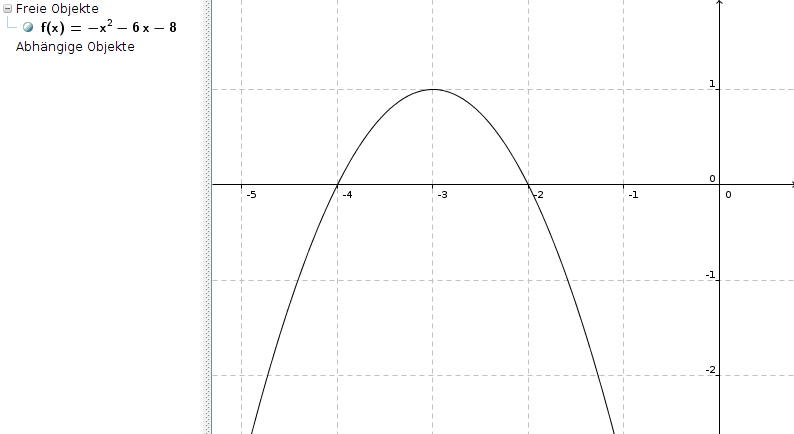
Scheitelpunkt:

f'(x) = - 2x - 6 = 0

x = -3

f(-3) = - 9 + 18 - 8 = -1

S(-3|1)

 

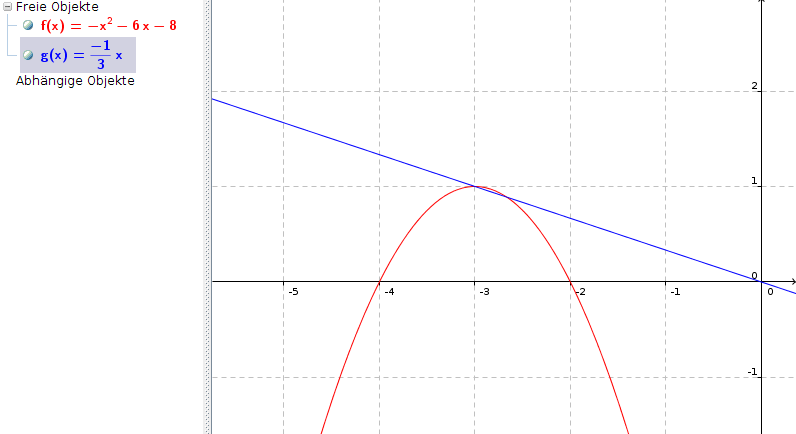
Gleichung der Verbindungsgeraden vom Scheitelpunkt der Parabel zum Koordinatenursprung:

Diese geht durch (-3|1) und (0|0), also

m = (0-1)/(0-(-3)) = -1/3

y = mx + b

0 = -1/3 * 0 + b

b = 0

Die Verbindungsgerade kann also durch folgende Gleichung beschrieben werden:

g(x) = -1/3 * x

 

Besten Gruß

Comments

Vielen dank, es hat mir sehr weiter geholfen.

Answer 2

Eine nach unten geöffnete Normalparabel schneidet die x Achse bei x1 = -2 und bei x2 = -4.

Funktionsgleichung direkt f(x) = -(x+2)(x+4)                                            
a) Ermittle die Funktionsgleichung der Parabel, deren Scheitelpunktform und  

f(x) = -(x+2)(x+4)   = -(x^2 + 6x + 8)    quadr. Ergänzung

=-(x^2 +6x + 9 -9 +8)    

= -( (x+3)^2   -1)

= -(x+3)^2 +1

Scheitelpunkt S(-3|1)                                                        
 b) die Gleichung der Verbindungsgeraden vom Scheitelpunkt der Parabel zum Koordinatenursprung.

y= -1/3 x