Aufgabe:
Sei \( \mathbb{K} \) ein Körper und \( V, W \mathbb{K} \)-Vektorräume. Es sei \( \left\{v_{1}, \ldots, v_{m}\right\} \) eine Basis von \( V \) und \( \left\{w_{1}, \ldots, w_{n}\right\} \) eine Basis von \( W . \) Wir definieren die Abbildungen
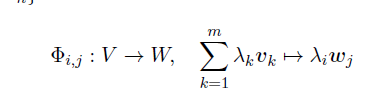
Text erkannt:
\( \Phi_{i, j}: V \rightarrow W, \quad \sum \limits_{k=1}^{m} \lambda_{k} v_{k} \mapsto \lambda_{i} w_{j} \)
für \( i=1, \ldots, m, j=1, \ldots, n \). Zeigen Sie, dass dann
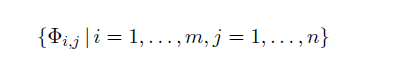
eine Basis des Vektorraums \( L(V, W) \) ist.
Kann mir wer helfen dies zu losen weil ich nicht so ganz verstehe wie ich diese berechne.
Ich weiss dass man die wohldefinierheit nachweisen soll, aber habe lieder kein Plan wie