Aufgabe:grenzwert berechnen
…
Problem/Ansatz: Wie kommt man hier auf 1/1+k,denn wenn es die geometrische Reihe ist, müsste es ja 1/1-q sein.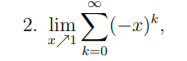
Text erkannt:
2. \( \lim \limits_{x \nearrow 1} \sum \limits_{k=0}^{\infty}(-x)^{k} \),

Text erkannt:
1. Nach Aufgabe U41 gilt für jedes \( x>0 \)
\( \log (x) \leq x-1 \leq x \)
Für \( x \geq 1 \) ist damit
\( 0 \leq \frac{\log (x)^{2}}{2^{x}} \leq \frac{x^{2}}{2^{x}} \stackrel{x \rightarrow \infty}{\longrightarrow} 0 \)
also \( \lim \limits_{x \rightarrow \infty} \frac{\log (x)^{2}}{2^{x}}=0 \).
2. Für \( x \in(0,1) \) gilt
\( \sum \limits_{k=0}^{\infty}(-x)^{k}=\frac{1}{1+x} \)