Bernoulli-Ungleichung | Sandwichkriterium bei Folgen

Question

Ich habe folgende Folge gegeben:

(an)n∈ℕ mit an = ((1)  -1/n^2)^2

ich soll den grenzwert angeben, das hab ich auch getan:

\( \lim\limits_{n\to\infty} \) ((1) - 1/n^2)^2 = 1,

Zum Beweis soll ich die Bernoulli Ungleichung verwenden :

Sei x ≥ -1 dann gilt:

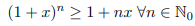
Dazu soll ich das Sandwich Kriterium verwenden.

Zur Bernoulli ungleichung:

müsste ich dann hier das nicht so umändern =

((1) - 1/n^2)^2 ≤ 1 + nx ∀n ∈ ℕ₀

Falls das bis hierher richtig sein sollte, wie fahre ich genau weiter fort?

Answer 1

Hallo :-)

Du hast falsch gerechnet. Setze doch mal den Ausdruck \((1-\frac{1}{n^2})^n\) passend in die Ungleichung ein. Schreibe es dazu so um:

$$ \left(1-\frac{1}{n^2}\right)^n=\left(1+\underbrace{\left(-\frac{1}{n^2}\right)}_{=:x}\right)^n $$

Comments

Hmm, Alles klar aber wie mache ich dann weiter bin etwas verwirrt.

---

Was hast du denn gerechnet?

---

nocht nicht wirklich was, deshalb bin ich ja verwirrt wie genau ich ab dem punkt weiter mache, tut mir leid.

---

Du musst dich nur noch die Bernoullie Ungleichung anwenden. Rechne das mal aus.

---

ok, wenn ich das richtig verstanden habe dann so:

(1 + (-1/n^2))^2 ≤ 1 + (-1/n)

?

---

Ich sehe gerade, dass deine Folge für Bernoullie nicht geeignet ist. Für den Ausdruck \(\left(1-\frac{1}{n^2}\right)^n\) eignet sie sich aber ganz gut.

---

Deine Aufgabe ist wahrscheinlich falsch abgetippt, da sich deine Folge für Bernoullie nicht eignet.

---

ja genau die Folge war gemeint, hatte mich vertippt sorry!

---

Sieht du denn jetzt, wie die Ungleichung anzuwenden ist?

---

wie genau ich sie anwende verwirrt mich gerade, ich habs ja eingesetzt, aber wie rechne ich dann weiter bzw, was muss ich beachten.

---

achso, bevor ich es vergesse habs geschafft:

1 - 1/n ≤ (1+ (-1/n^2))^n ≤ 1

---

Genau! Wie lautet der Grenzwert deiner unteren Abschätzung \(1-\frac{1}{n}\)?

---

Konvergiert gegen 1, meinen sie das?

---

Ja, genau.________

---

Ja, genau._______________

---

Danke nochmal für all die Hilfe von ihnen !