Bevor man losrechnet, macht man sich tunlichst zunächst eine Skizze:
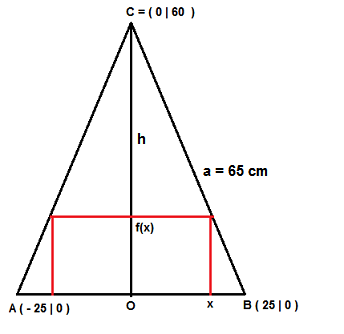
In dieser Skizze ist das Dreieck so in ein Koordinatensystem gelegt, dass seine Basis auf der x-Achse und der Fußpunkt seiner Höhe h im Koordinatenursprung O liegt.
Die y- Koordinate des Punktes C ist dann gleich der Länge der Höhe h. Diese ergibt sich nach dem Satz des Pythagoras zu:
h = √ ( 65 2 - 25 2 ) = √ 3600 = 60
Für den von x abhängigen Flächeninhalt A des rot eingezeichneten Rechtecks gilt dann:
A ( x ) = 2 * x * f ( x )
wobei f ( x ) die Gleichung der Geraden BC ist. Diese lässt sich mit der Achsenabschnittsform einer Geraden schnell bestimmen: Die Gerade schneidet die x -Achse an der Stelle x = 25 und die y- Achse an der Stelle f ( 0 ) = 60. Es gilt also:
f ( x ) / 60 + x / 25 = 1
<=> f ( x ) = ( 1 - x / 25 ) * 60
= - 2,4 x + 60
Somit gilt für A:
A ( x ) = 2 * x * f ( x )
= 2 * x * ( - 2,4 x + 60 )
= - 4,8 x 2 + 120 x
Zur Bestimmung des maximalen Flächeninhaltes Amax muss die Stelle x bestimmt werden, an der A ( x ) ein Maximum annimmt, also:
Nullsetzen der ersten Ableitung von A ( x ) und Auflösen nach x:
A ' ( x ) = - 9,6 x + 120 = 0
<=> 9,6 x = 120
<=> x = 120 / 9,6 = 12,5
Da A ' ' ( x ) = - 9,6 überall negativ ist, also insbesondere auch an der Stelle x = 12,5, liegt dort tatsächlich ein Maximum von A ( x ) vor.
Das Rechteck mit dem maximalen Flächeninhalt hat somit die Breite
2 * 12,5 = 25 cm
und die Höhe
f ( 12,5 ) = 30 cm
Der maximale Flächeninhalt Amax ist:
Amax = A ( 12,5 ) = - 4,8 * 12,5 2 + 120 * 12,5 = 750 cm 2
oder einfach, da es sich um ein Rechteck handelt:
Amax = Breite * Höhe = 25 * 30 = 750 cm 2