Intervallschachtelung zeigen | Intervall Folgen

Question

Ich habe ein abgeschlossenes Intervall I_n = [1 - (1/2)ⁿ , 1 + 1/n²] , n ∈ ℕ

Ich soll nun zeigen, dass I_n eine Intervallverschachtelung ist.

dies soll ich dazu beachten:

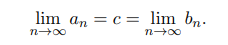
ich hab mir nun gedacht:

\( \lim\limits_{n\to\infty} \) (1 - (1/2)ⁿ ) = 1

\( \lim\limits_{n\to\infty} \) (1 + 1/n²)    = 1

c = 1

=> (1 - (1/2)ⁿ) ≤ 1 ≤ (1 + 1/n²)

Darf ich das so zeigen, oder muss ich das anders machen?

Danke im voraus.

Answer 1

Du musst zeigen, dass \( a_{n} \) monoton steigend und \( b_{n} \) monoton fallend ist und dass \( a_{n} \leq b_{n} \) für alle \( n \in \mathbb{N} \) gilt. Aussderdem musst du zeigen, dass \( d_{n}=b_{n}-a_{n} \) eine Nullfolge ist. Daraus kannst du dann schliessen, da ja \( a_{n} \) und \( b_{n} \) konvergieren (Bolzano Weierstrass), dass
\(\begin{aligned} \lim \limits_{n \rightarrow \infty} d_{n}=0 \Longleftrightarrow \lim \limits_{n \rightarrow \infty}\left(b_{n}-a_{n}\right)=0 \Longleftrightarrow \lim \limits_{n \rightarrow \infty} b_{n}=\lim \limits_{n \rightarrow \infty} a_{n}\end{aligned} \)
(Die letzte Äquivalenz folgt nur, da wir wissen, dass die beiden Folgen konvergieren!).