Hallo Roland,
wenn man die ganze Figur achtelt, bleibt von der Fläche des Sterns das grün markierte Dreieck \(\triangle ABC\) übrig.
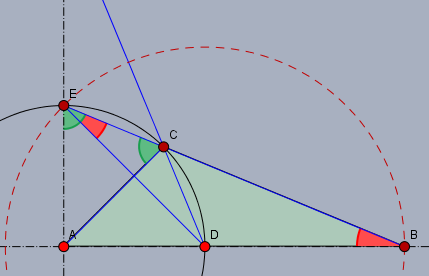
Das gleichschenklige Dreieck \(\triangle ADC\) ist ein Achtel des Achtecks. Beide Dreicke haben eine gemeinsame Höhe über \(AB\). Das gesuchte Flächenverhältnis \(\tau\) ist dann offensichtlich$$\tau = \frac{F_{ADC}}{F_{ABC}} = \frac{|AD|}{|AB|}$$Die Winkel \(\angle DEC\) und \(\angle CBA\) (beide rot) sind gleich groß, was sich über die Winkelsumme in den Dreiecken \(\triangle ACE\), \(\triangle ADE\) und \(\triangle ABE\) zeigen lässt. Folglich ist auch $$|DB| = |DE| = |AD| \cdot \sqrt 2$$Und damit ist das gesuchte Verhältnis$$\tau =\frac{|AD|}{|AB|} = \frac{|AD|}{|AD|+|DB|} = \frac{1}{1+\sqrt 2} = \sqrt 2 - 1$$Gruß Werner