Berechne die Länge der Strecke r und b. Prismenförmige Schachtel

Question

Aufgabe:

Zum Verpacken von Geschenken werden prismenförmige Schachteln mit unterschiedlichen Höhen benutzt. Die Grundflächen dieser Schachteln sind regelmäßige Achtecke mit der Seitenlänge a= 6,0cm.

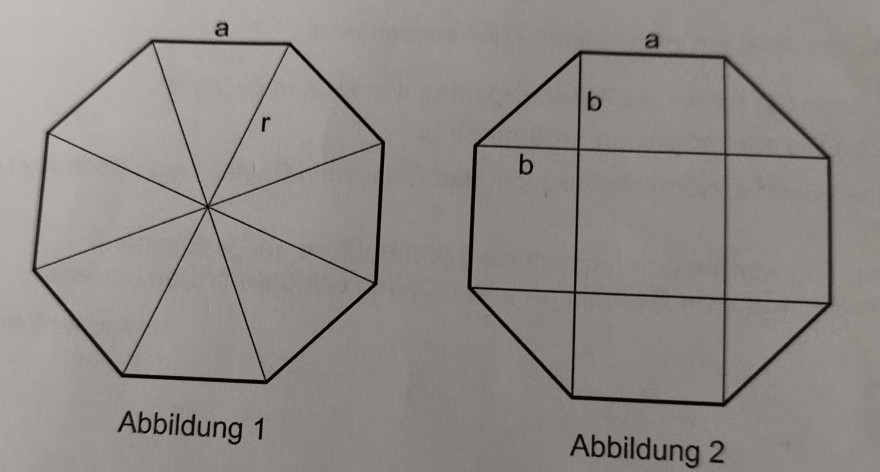
Ein solches Achteck kann unterschiedlich zerlegt werden.

a) Berechne die Länge der Strecke r. (s.Abbildung1)

b) Berechne die Länge der Strecke b.( s.Abbildung 2)

Problem/Ansatz:

Ich brauche bitte Hilfe wie ich das berechnen kann. Mein Ansatz für b ist:

b²+b²=a²

2b²=8²

2b²=64

b²=32

b=5,7cm

Für r habe ich keinen Ansatz.

Text erkannt:

Abbildung 1
Abbildung 2

Comments

wenn du in a) eines der Teildreiecke vom Mittelpunkt aus mit der Winkelhalbieren in zwei rechtwinklige Teildreiecke zerlegst, hast du bei diesen die Seiten a/2 und den Mittelpunktswinkel 360°/8/2. Daraus kannst du r ausrechnen.

Answer 1

\(\sin(22,5°)=\frac{3}{r}\)

\(r=\frac{3}{\sin(22,5°)}\)

Comments

Was sehe ich falsch?

---

\(r=\frac{3}{\sin(22,5°)}≈7,839\)

---

Wie komme ich auf diese Rechnung? Ich würde das gern nachvollziehen zum lernen.

Und kann mir jemand sagen , ob ich b richtig gemacht habe ?

---

du hast bei b) wohl a=8  statt a=6 eingesetzt

---

\(r=\frac{3}{\sin(22,5°)}≈7,839\)

$$r = \frac{a}{\sqrt{2-\sqrt{2}}}= \frac{a}{2}\sqrt{4+2\sqrt{2}}$$

Wie komme ich auf diese Rechnung? Ich würde das gern nachvollziehen zum lernen.

stelle für das rot markierte Dreieck den Pythagoras auf. Hinweis:$$|MP| = |PA| = \frac{r}{2}\sqrt{2}$$

---

oder die Aufgabenteile in der Reihenfolge erst b), dann a) bearbeiten

---

Wo liegt mein Fehler mit dem sin-Ansatz?

---

Der Ansatz ist richtig.

---

dein Ansatz ist richtig  (Tippfehler?)

---

Du hast Dich verrechnet.

---

Danke. Wo bitte? Ich finde den Fehler nicht.

---

Ich finde den Fehler nicht.

wir auch nicht!

sin45°/6 = sin67,5°/r

ok!

r = 8,88 cm

nicht ok ...

Du wirst Dich wohl schlicht irgendwo verrechnet haben$$\begin{aligned} \sin45°/6\text{cm} &= \sin67,5°/r \\ r &=  6\text{cm}\cdot \frac{\sin67,5°}{\sin45°}= 6\text{cm}\cdot\frac{\frac{1}{2}\sqrt{2+\sqrt{2}}}{\frac{1}{2}\sqrt{2}}\\ &= 6\text{cm}\cdot \frac{1}{2}\sqrt{4+2\sqrt{2}} \approx 6\text{cm}\cdot 1,3066\\ &\approx 7,839\text{cm} \end{aligned}$$

---

Ja, das ist beim Ausrechnen etwas schiefgelaufen.

Beim 3. Mal hat es geklappt.

Answer 2

a) Mittelpunktswinkel 360°/8 = 45°

Die anderen Winkel betragen je (180°-45°) /2 = 67,5°

sin45°/6 = sin67,5°/r

r = 8,88 cm

Comments

Man kommt hier ohne Winkel (und nachfolgende Trigonometrie) aus und vielleicht soll man das sogar.

---

Ja, mit Pythagoras ist das ein ziemliches Wurzel-in-Wurzel-Gewusel.

Es gilt \(r=\frac{a}{\sqrt{(\frac{\sqrt{2}}{2})^2+(1-\frac{\sqrt{2}}{2})^2}}\).

---

Also besser ohne Pythagoras? Das ist eine Prüfungsaufgabe zum üben, ich möchte es nur bestmöglich lernen.

---

Jetzt weiß ich nicht was nun richtig ist. 7,8 siehe oben die Rechnung  oder 8,8 .

---

≈ 7,8 ist richtig (Antwort Moliets)

---

Lieben Dank. Ich probier das jetzt alles mal erstmal aus und versuche es zu verstehen.

Kann mir jemand sagen, ob ich Strecke b richtig gerechnet habe?

---

Du hast bei b)  wohl a=8 statt a=6  eingesetzt

---

Das hat mir sehr geholfen und ich hab nun auch verstanden wie ich r berechnen kann bzw. konnte es nachvollziehen. Vielen vielen Dank dafür.

Ich habe noch eine Frage. Ich muss ein senkrechtes Zweitafelbild zeichnen von dieser Schachtel. Und die Schachtel ist 5 cm hoch. Wie kann ich da vorgehen? Gehe ich von einem Prisma/ Achteck aus?