Funktion f mit f(x) = ax² + bx + c -> Parabel

Question

Kann mir jemand schnellst wie möglich diese Lösungen mit LGS zeigen?

Bitte zeigen Sie für diese Lösungen für Anfänger, da ich Anfängerin bin ..


Berechnen Sie für die Funktion f mit f(x) = ax² + bx  + c die Koeffizienten a, b, c so dass die angegebenen Punkte auf dem zugehörigen Graphen liegen. Ermitteln Sie dann den Scheitel der Parabel und geben Sie die Öffnungsrichtung an.


a) P(0/0) ; Q(3/-3) ; R(1/5)


b) P(1/0) ; Q(-1/0) ; R(2/1)


c) P(0/-2) ; Q(-1/1) ; R(2/6)

Answer 1

 

f(x) = ax² + bx  + c

 

a)

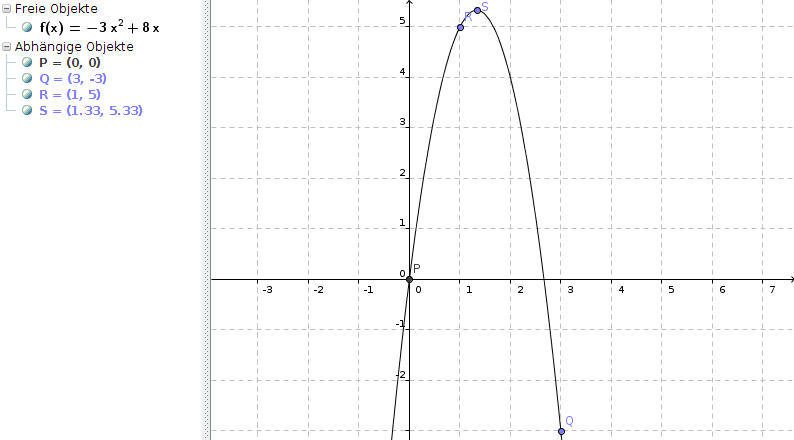
P(0/0) ; Q(3/-3) ; R(1/5)

Diese Punkte liegen auf der Parabel; wir setzen sie alle in die Funktionsgleichung ein:

I. f(0) = a * 0² + b * 0 + c = 0, also c = 0

II. f(3) = a * 3² + b * 3 + c = -3, also 9a + 3b + c = -3, also, da c = 0: 9a + 3b = -3

III. f(1) = a * 1² + b * 1 + c = 5, also a + b = 5, also a = 5 - b

Wir setzen III. in II. ein:

9a + 3b = - 3

9 * (5 - b) + 3b = -3

45 - 9b + 3b = -3

-6b = -48

b = 8

Das setzen wir in II. ein

9a + 24 = -3

9a = -27

a = -3

Die Funktionsgleichung lautet also

f(x) = -3x² + 8x

An dem Minuszeichen -3x² erkennt man, dass die Parabel nach unten geöffnet ist.

Den Scheitel kann man gut finden, indem man die erste Ableitung f'(x) = 0 setzt:

f'(x) = -6x + 8 = 0

-6x = -8

x = 8/6 = 4/3

Das in die Ursprungsfunktion eingesetzt ergibt den entsprechenden y-Wert:

f(8/6) = - 3 * (8/6)² + 8 * (8/6) = 16/3

Scheitelpunkt S = (4/3|16/3)

 

Die anderen Aufgaben werden genauso gerechnet :-)

 

Für die Lösung der LGS kannst Du entweder das Einsetzverfahren nutzen, wie ich es getan habe, oder den Gauss-Algorithmus oder einen guten Taschenrechner :-)

 

Besten Gruß

Comments

also ich habe selbstständig gemacht und leider ist das Ergebnis anders:

P(0/0)
f(x) = a*0² + b*0 + c = 0
f(x) = c = 0

Q(3/-3)
f(x) = a*3² + b*3 + c = -3
f(x) = 9a + 3b + c = -3

R(1/5)
f(x) = a*1² + b*1 + c = 5
f(x) = a + b + c = 5

I                       c = 0    |einsetzen in II und III
II    9a + 3b + c = -3
III   a   +  b   + c = 5

II    9a + 3b + 0 = -3  | -0
III   a   +  b   + 0 = 5   | -0

II    9a + 3b        = -3  | *1  (minus)
III   a   +  b         = 5   | *3

II    9a + 3b        = -3
III   6a                 = 5   | :6

II    9a + 3b        = -3
III   a                   = 5/6   | einsetzen in II

II    -7,5 + 3b      = -3    | +7,5

II                3b      = -10,5    | : 3

II                  b       =  -3,5
f(x) = -5/6x² - 3,5x ... warum liegt dann da eine fehler? :(

---

Bis hierhin war alles richtig:

II    9a + 3b        = -3  | *1  (minus)
III   a   +  b         = 5   | *3

II    9a + 3b        = -3
III   6a                 = 5   | :6

 

Hier muss es heißen:

II 9a + 3b = -3

III 6a = -3 - 15 = -18, also a = -3

Denn Du hast ja III mit 3 multipliziert und von II subtrahiert, also wird auch die 5 rechts neben dem Gleichheitszeichen mit 3 multipliziert! Dieser Fehler zieht sich jetzt durch den Rest Deiner Berechnungen:

II    9a + 3b        = -3
III   a                   = -3 | einsetzen in II

II    -27 + 3b      = -3    | +27

II                3b      = 24    | : 3

II                  b       =  8
 

Besten Gruß

---

Danke sehr .. Ich hab jetzt auch geschafft Aufgbe b und c zu lösen :-) .. Gute Nacht :-) ..

---

Klasse, das freut mich!

Gern geschehen - und auch Dir eine gute Nacht :-)

Brucybabe

---

Was macht man mit dem c bei aufgabe b? bei a ist c= 0 und bei b komm ichnicht darauf wiedie lösung ist .. können sie bitte auch die aufgabe b zeigen ?

---

Ja sicher :-)

 

f(x) = ax² + bx  + c

b) P(1/0) ; Q(-1/0) ; R(2/1)

 

I. f(1) = a + b + c = 0

II. f(-1) = a - b + c = 0

III. f(2) = 4a + 2b + c = 1

 

I. - II.

2b = 0 | b = 0

 

III. - 4 * I.

-3c = 1

c = -1/3

 

Das eingesetzt in zum Beispiel I.

a + (-1/3) = 0

a = 1/3

 

Damit lautet die Funktion

f(x) = 1/3 * x² - 1/3

Positiver Koeffizient von x², also Parabel nach oben geöffnet.

f'(x) = 2/3 * x = 0

x = 0

Scheitelpunkt (0|f(0)), also

S = (0|-1/3)

 

Besten Gruß