Aufgabe:
Die Pummerin ist die größte Glocke im Wiener Stephansdom. Ihr Querschnitt wird näherungsweise durch den Graphen der Funktion f(x) = 0,4 . x 4 + 1,8 . x2 + 2,3 beschrieben (Maße in m).
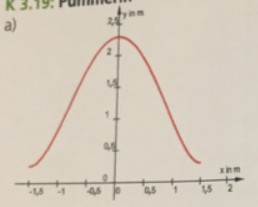
a) Zeichnen Sie den Funktionsgraphen und geben Sie einen sinnvollen Definitionsbereich an.
b) Ermitteln Sie die Höhe der Pummerin.
c) Lesen Sie aus dem Graphen ab, wie breit die Glocke in 1,5 m Höhe ist. Beschreiben Sie, wie Sie diese Breite rechnerisch ermitteln können.
Problem/Ansatz:
Bei a) bekomme ich nämlich bei Eingabe in den graphikfähigen Rechner eine nach oben offene Parabel, diese stimmt jedoch nicht mit dem Graph des Lösungshefts überein (siehe Abb.).
Bei c) weiß ich, dass ich f(x) = 1.5 setzen muss, um die genaue Breite der Glocke zu erhalten, ich weiß jedoch nicht, wie die Funktion umgeformt werden muss, um diese Berechnung anstellen zu können.