Aufgabe:
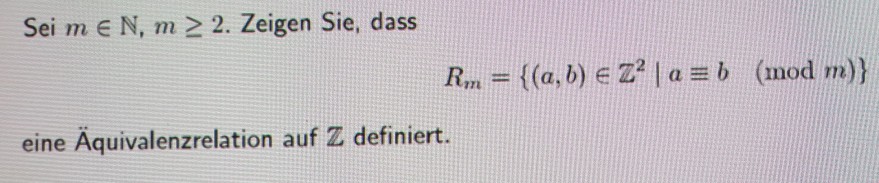
Text erkannt:
Sei \( m \in \mathbb{N}, m \geq 2 \). Zeigen Sie, dass
\( R_{m}=\left\{(a, b) \in \mathbb{Z}^{2} \mid a \equiv b \quad(\bmod m)\right\} \)
eine Äquivalenzrelation auf \( \mathbb{Z} \) definiert.
Problem/Ansatz:
Das ist meine Lösung:
1. Reflexivität: ∀a ∈ Z: a≡a (mod a)
2. Symmetrie: ∀a, b ∈ Z: a≡b (mod m) ⇒ b ≡ a (mod m)
3. Transitivität: ∀a,b,c ∈ Z: a ≡ b (mod m) ∧ b ≡ c (mod m) ⇒ a ≡ c (mod m).
Ist das richtig?