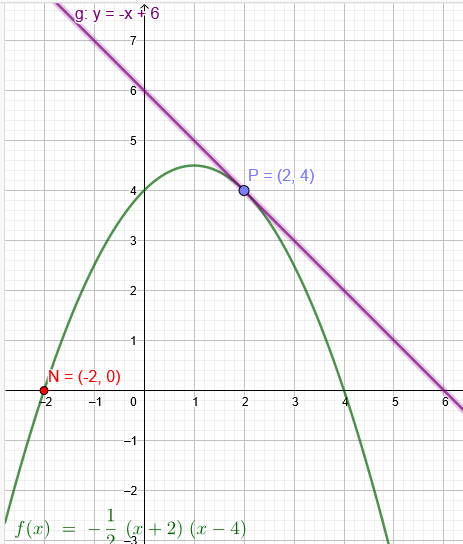
"a) Bestimmen Sie die Koeffizienten a, b und c in der Funktionsgleichung so, dass die Parabel durch den Punkt P(2|4) verläuft, im Punkt P die Steigung -1 hat und weiterhin die x-Achse bei x = -2 schneidet."
Weg über die Nullstellenform der quadratischen Parabel:
f(x)=a*(x-(-2)*(x-N)=a*(x+2)*(x-N)
P(2|4)
f(2)=a*(2+2)*(2-N)=4a*(2-N)
1.) 4a*(2-N)=4 → a*(2-N)=1 → a=\( \frac{1}{2-N} \)
f(x)=\( \frac{1}{2-N} \)*[(x+2)*(x-N)]
f´(x)=\( \frac{1}{2-N} \)*[1*(x-N)+(x+2)*1]=\( \frac{1}{2-N} \)*[2x-N+2]
f´(2)=\( \frac{1}{2-N} \)*[2*2-N+2]=\( \frac{1}{2-N} \)*[6-N]
2.)\( \frac{1}{2-N} \)*[6-N]=-1 → [6-N]=-1*(2-N)→ 6-N=N-2 → N=4
f(x)=\( \frac{1}{2-4} \)*(x+2)*(x-4)=-\( \frac{1}{2} \)*(x+2)*(x-4)
Ausmultiplizieren: a=... b=... c=...