Hallo Roland,
hj schrieb:
Als ersten Schritt zur Lösung solltest du ähnliche Dreiecke suchen.
das sind so viele, dass man sich gar nicht entscheiden kann ;-) Es gibt bestimmt ein gefühltes Dutzend Möglicheiten das Verhältnis der beiden Flächen zu berechnen. Ich habe 'ne Weile gesucht, bis ich eine Lösung gefunden habe, die sich nur auf Ähnlichkeiten abstützt.
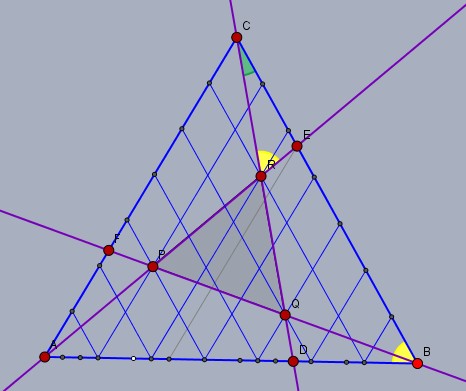
Dazu führe ich ein Raster aus äquidistanten und zu den Seiten parallelen Geraden ein, so dass die Seiten in 21 gleich lange Strecken unterteilt werden. Bem.: es sind oben nicht alle Geraden des Rasters eingezeichnet!
Das führt dazu, dass die Ecken des grauen Dreiecks \(\triangle PQR\) auf Gitterpunkten dieses Rasters liegen. Wegen der Drehsymmetrie ist das \(\triangle PQR\) gleichseitig; seine Seitenlänge sei \(|PQ|=s\). Die Seitenlänge des großen Dreiecks \(\triangle ABC\) sei \(|AB|=3a=l\)
Aus dem Raster lässt sich unmittelbar ablesen:$$|QD| = |RE| = \frac 13 s\\|CR|=|QR|=s=\frac 37|CD|$$Die beiden Dreiecke \(\triangle DBC\) und \(\triangle REC\) sind ähnlich. Folglich gilt$$\begin{aligned}\frac{|CR|=s}{|CE|=\frac 13l} &= \frac{|CB|=l}{|CD| = \frac73s}\\ \implies\frac{s^2}{l^2}&= \frac{\frac 13}{\frac73} = \frac 17\end{aligned}$$Und \(s^2/l^2\) ist auch das gesuchte Verhältnis der beiden Flächen. Somit ist $$F_{\triangle PQR} = \frac 17 F_{\triangle ABC}$$Gruß Werner