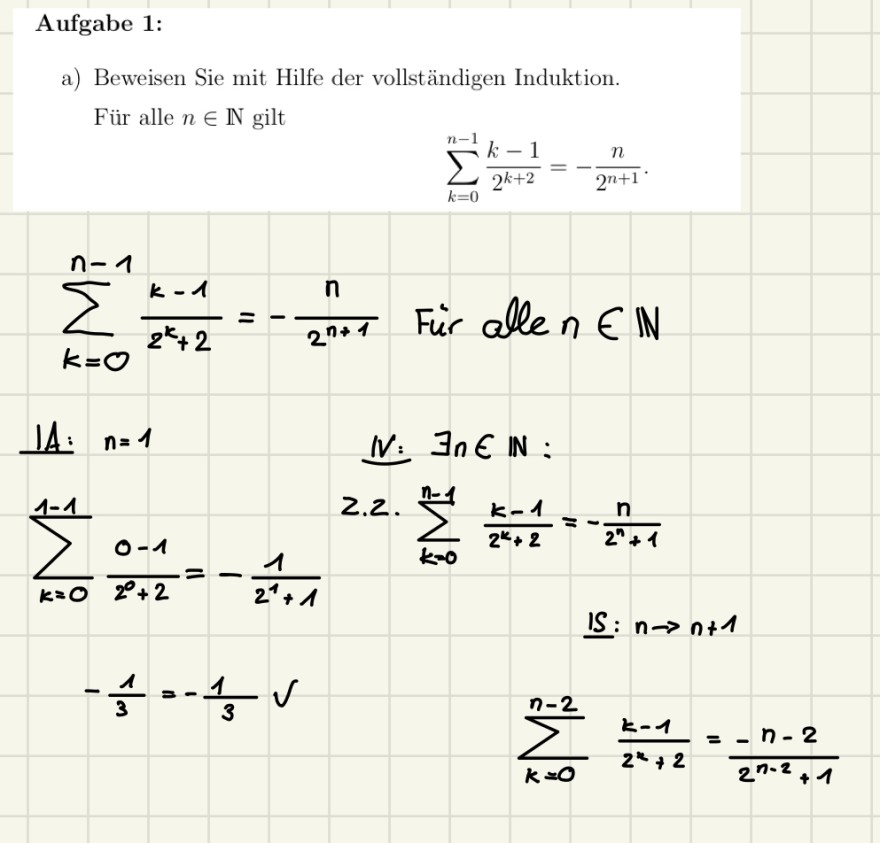
Text erkannt:
Aufgabe 1:
a) Beweisen Sie mit Hilfe der vollständigen Induktion.
Für alle \( n \in \mathbb{N} \) gilt
\( \sum \limits_{k=0}^{n-1} \frac{k-1}{2^{k+2}}=-\frac{n}{2^{n+1}} . \)
Fur allen\in\mathbb\mathbbN
\existsn\in \( \mathbb{N}: \)
\( \sum \limits_{k=0}^{n-1} \frac{k-1}{2^{k}+2}=-\frac{n}{2^{n}+1} \)
\( \frac{15: n \rightarrow n+1}{k-2} \)
\( \sum \limits_{k=0}^{n} \frac{k-1}{2^{k}+2}=\frac{-n-2}{2^{n-2}+1} \)
Aufgabe
Vollständige Induktion letzter Schritt n-1 wird zu ?
Problem/Ansatz:
Ansätze als Foto brauche bitte die Lösung komm nicht weiter.