Wie groß ist die Wahrscheinlichkeit für ein Ergebnis unter 100?

Question

Aufgabe:

Du hast drei Würfel, die du einmal würfelst.

Du merkst dir die Gesamtzahl der Augen dieses Wurfs.

Danach würfelt man diese drei Würfel erneut, addiert wieder alle Augen zusammen und multipliziert diese Summe mit dem Ergebnis des ersten Wurfs.

Wie groß ist die Wahrscheinlichkeit für ein Ergebnis unter 100? (auf ganze Prozente aufrunden)

Answer 1

Ich würde mir zunächst die Fälle notieren, bei der man auf ein "Augensummenprodukt" von unter 100 kommt:

3 und [3, 18]
4 und [3, 18]
5 und [3, 18]
6 und [3, 16]
7 und [3, 14]
8 und [3, 12]
9 und [3, 11]
10 und [3, 9]
11 und [3, 9]
12 und [3, 8]
13 und [3, 7]
14 und [3, 7]
15 und [3, 6]
16 und [3, 6]
17 und [3, 5]
18 und [3, 5]

Ich hoffe, es ist kein Fehler drin. Aber das könntest du ja als erstes überprüfen.

Comments

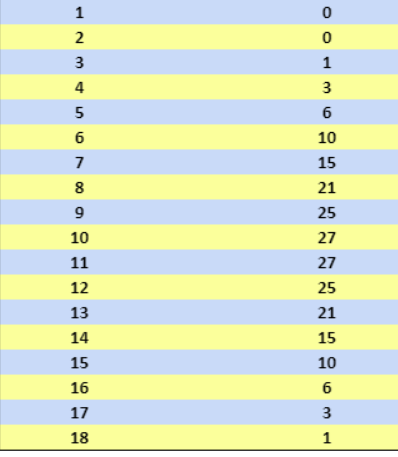
Spalte 1 : Anzahl der Augen bei einem Wurf mit drei Würfeln

Spalte 2 : Anzahl der Möglichkeiten diese Augenzahl zu erreichen.

Um den angeforderten Prozentsatz zu berechnen, müssen Sie die Anzahl der "gültigen" Kombinationen und die Anzahl der Gesamtkombinationen kennen.

Die Gesamtzahl der Kombinationen ist angegeben.

Was sind dann gültige Kombinationen?

Angenommen, Sie würfeln beim ersten Wurf insgesamt sechs.
Dies kann auf 10 verschiedene Arten erfolgen (siehe Tabelle).

Wurf zwei darf dann maximal 16 Augen haben (weil ( 6 * 16=96 ) und damit knapp unter 100).

Für Wurf zwei sind dies also 1+3+6+10+15+21+25+27+27+25+21+15+10+6=212  Möglichkeiten.

Die Anzahl möglicher gültiger Kombinationen für einen ersten Wurf von sechs Augen beträgt daher: 10 * 212 = 2120

Berechnen Sie nun die Anzahl gültiger Kombinationen für andere 'erste Würfe' und Sie können dann das Gewünschte tun Prozent berechnen.

216 ist die Gesamtzahl der verschiedenen Möglichkeiten, drei Würfel einmal zu würfeln

46656 ist die Gesamtzahl der verschiedenen Möglichkeiten, drei Würfel zweimal zu würfeln