Stammfunktion, Flächenberechnung

Question

Aufgabe:

6 Gegeben ist die Funktion \( f \) mit \( f(x)=10 x \cdot e^{-\frac{1}{2} x} \)
c) Zeigen Sie, dass \( F \) mit \( F(x)=-20(x+2) \cdot e^{-\frac{1}{2} x} \) eine Stammfunktion von \( f \) ist.
d) Berechnen Sie mithilfe von \( \mathrm{F} \) den Inhalt der Fläche, die von \( \mathrm{f} \) mit den Koordinatenachsen und der Geraden mit der Gleichung \( x=10 \) eingeschlossen wird.
e) Der Graph von f schließt mit der x-Achse auf dem Intervall \( [0 ; \) a] eine Fläche ein. Für welchen Wert von a beträgt der Flächeninhalt 35 ?

Problem/Ansatz:

Ich bin komplett am verzweifeln weil ich einfach nicht auf die Ableitung komme obwohl ich die Kettenregel anwende aber iwie kommt immer was anderes raus und ich verstehe auch nicht wie ich d) rechnen soll.

Könnte mir jemand die Lösungen dazu sagen?

Weil alleine bekomme ich das echt nicht hin wenn das keiner vorrechnet und brauche die Lösungen für morgen.

Wäre mega nett!!

Answer 1

\( F(x)=-20(x+2) \cdot e^{-\frac{1}{2} x} \)

Der Funktionsterm ist ein Produkt. Deshalb wird es mit der Produktregel abgeleitet.

Comments

Ja das meinte ich auch eigentlich, trotzdem komme ich auf kein Ergebnis

---

Ja das meinte ich auch eigentlich, trotzdem komme ich auf kein Ergebnis

Wir können leider nicht beurteilen, woran das liegt.

Wir sehen deinen Lösungsweg nicht und können so auch den Fehler nicht lokalisieren.

Answer 2

Hallo,

vielleicht hilft dir diese Rechnung:

\(F(x)=-20(x+2)\cdot e^{-0,5x}=-20e^{-0,5x}(x+2)\\ \text{Produktregel}\\ f(x)=u'\cdot v+u\cdot v'\\ u=-20e^{-0,5x}\quad u'=10e^{-0,5x}\\ v=x+2\quad v'=1\\ f(x)=10e^{-0,5x}\cdot (x+2)-20e^{-0,5x}\\ =10xe^{-0,5x}+20e^{-0,5x}-20e^{-0,5x}\\ =10xe^{-0,5x}\)

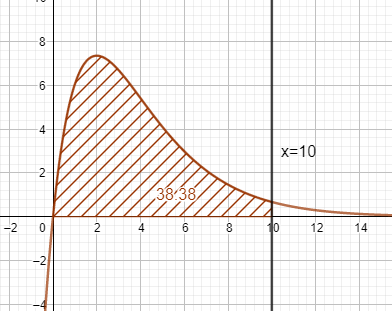
d) Berechnen Sie mithilfe von \( \mathrm{F} \) den Inhalt der Fläche, die von \( \mathrm{f} \) mit den Koordinatenachsen und der Geraden mit der Gleichung \( x=10 \) eingeschlossen wird.

Du sollst den Inhalt der schraffierten Fläche berechnen.

Guß, Silvia