Innere und äußere Tangenten zweier Kreise

Question

Aufgabe:

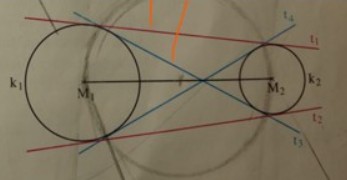
Betrachte die Figur rechts. Die beiden Tangenten \( t_{1} \) und \( t_{2} \) heißen äußere Tangenten an die beiden Kreise, die beiden Tangenten \( \mathrm{t}_{3} \) und \( \mathrm{t}_{4} \) innere Tangenten.

Zeichne zwei Kreise \( k_{1} \) und \( k_{2} \) mit \( r_{1}=2,1 \mathrm{~cm} \) und \( r_{2}=1,3 \mathrm{~cm} \). Der Abstand der beiden Mittelpunkte soll \( 5,2 \mathrm{~cm} \) betragen.

Problem/Ansatz:

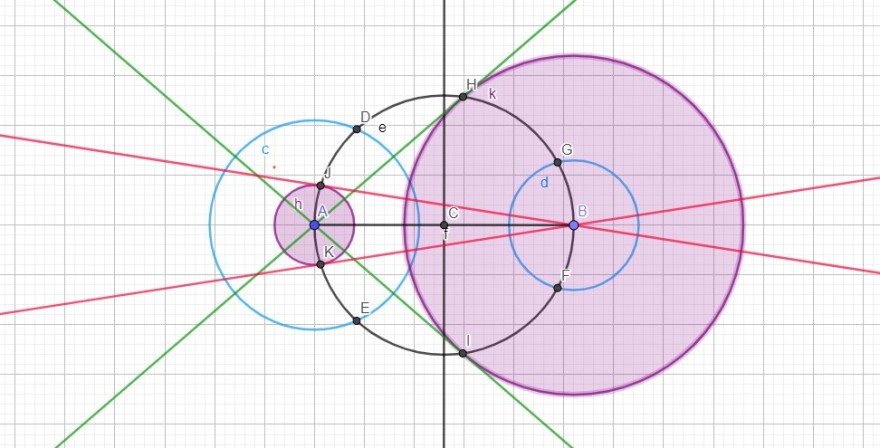
HAllo, habe VIEL überlegt OHNE Erfolg

Hast du ein Tipp wie kriege ich diese Tangenten GENAU O OHNE Geogebra? Nur mit Zirkel und Lineal usw...?

Habe so versucht

Answer 1

1. Zeichne die Gerade \(m\) durch die Mittelpunkte von \(k_1\) und \(k_2\).
2. Konstruiere die Senkrechte \(s_1\) zu \(m\) durch den Mittelpunkt von \(k_1\).
3. Zeichne einen Schnittpunkt \(S_1\) von \(s_1\) und \(k_1\).
   
4. Konstruiere die Senkrechte \(s_2\) zu \(m\) durch den Mittelpunkt von \(k_2\).
5. Zeichne den Schnittpunkt \(S_2\) von \(s_2\) und \(k_2\) ein, der auf der gleichen Seite von \(m\) liegt wie \(S_1\).
6. Zeichne die Gerade \(g\) durch \(S_1\) und \(S_2\).
7. Zeichne den Schnittpunkt \(P\) von \(g\) und \(m\).
8. Konstruiere die Tangente \(t\) von \(P\) an \(k_1\).
   

Die Gerade \(t\) ist auch Tangente von \(k_2\).

Die Idee hinter der Konstruktion ist, dass \(k_2\) aus \(k_1\) durch eine zentrische Streckung mit Streckzentrum \(P\) hervorgeht.

Comments

hast du es zeichnersich, Sprachlich KOMPLIZIERT