Aufgabe:
Die Klein'sche Vierergruppe ist jene 4-elementige Gruppe, deren Elemente \( \{1, a, b, c\} \) den Gleichungen \( a^{2}=b^{2}=1 \) und \( a b=c \) genügen. Gib die Operationstafel dieser Gruppe an.
Problem/Ansatz:
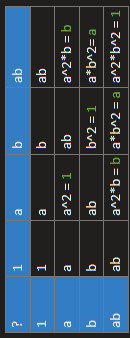
Text erkannt:
\begin{tabular}{|l|l|l|l|l|}
\hline\( ? \) & 1 & \( a \) & \( b \) & \( a b \) \\
\hline 1 & 1 & \( a \) & \( b \) & \( a b \) \\
\hline\( a \) & \( a \) & \( a^{\wedge} 2=1 \) & \( a b \) & \( a^{\wedge} 2^{*} b=b \) \\
\hline\( b \) & \( b \) & \( a b \) & \( b^{\wedge} 2=1 \) & \( a^{*} b^{\wedge} 2=a \) \\
\hline\( a b \) & \( a b \) & \( a^{\wedge} 2^{*} b=b \) & \( a^{*} b^{\wedge} 2=a \) & \( a^{\wedge} 2^{*} b^{\wedge} 2=1 \) \\
\hline
\end{tabular}
Meine Frage dazu wäre, wie finde ich heraus welche Operation man oben einsetzen muss. Kommt das aus der Angabe irgendwo hervor? Ich hätte jetzt mal mit * gerechnet.