¬((A∧ B) ⇒ (A∧ (B∨C))) ist eine Kontradiktion

Question

Aufgabe: ¬((A∧ B) ⇒ (A∧ (B∨C))) ist eine Kontradiktion

Problem/Ansatz:

Ist meine Lösung im Anhang so richtig? Wie zeige ich das am besten? Denn A und B und gleichzeitig nicht a oder nicht b kann ja nicht sein (die ersten beiden Klammern).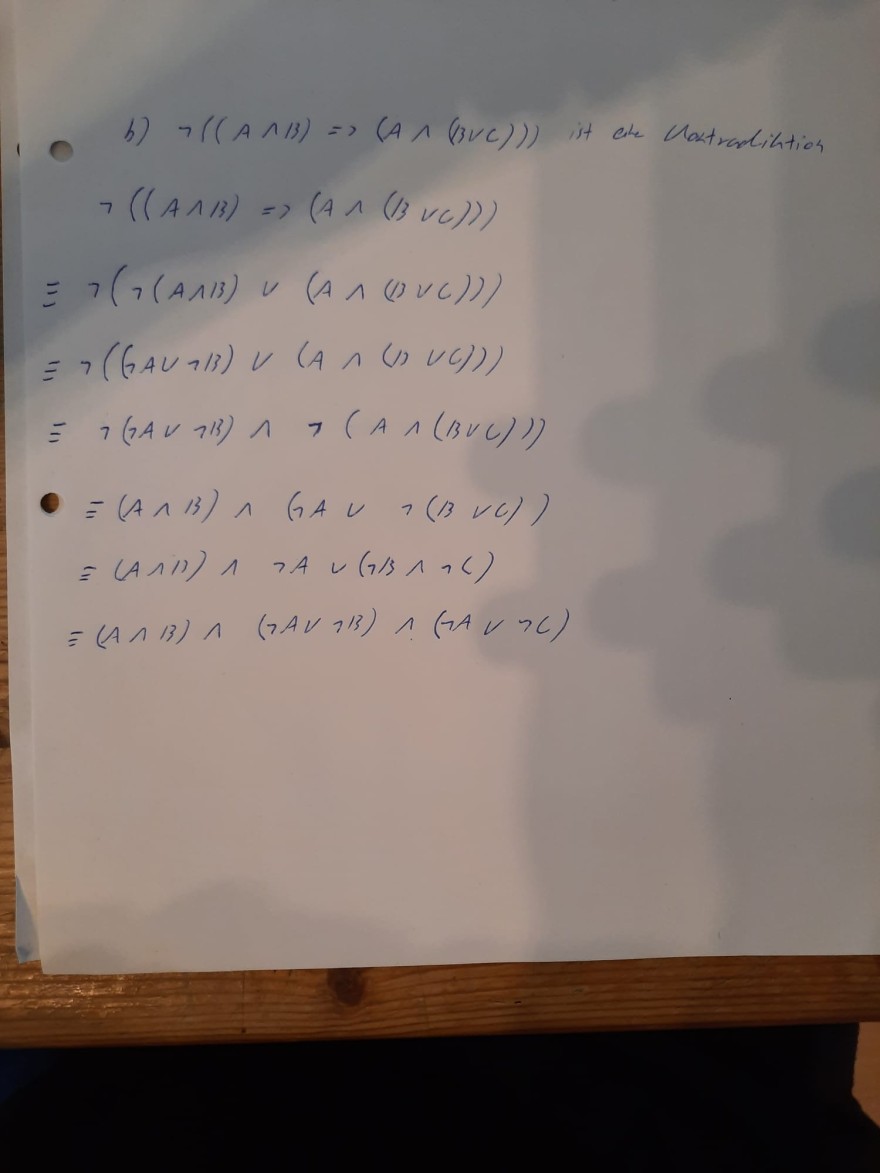

Text erkannt:

b) \( \neg((A \cap B) \Rightarrow(A \wedge(3 \vee C))) \) it che Maxtradihtion
\( 7((A \wedge 13) \Rightarrow(A \wedge(13 \vee C))) \)
\( \equiv 7(7(A \wedge 13) \cup(A \wedge(13 \vee C))) \)
\( \equiv((\neg A \cup \neg / 3) \vee(A \cap(1, V C))) \)
\( \equiv 7(7 A \cup 7 B) \wedge>(A \wedge(B V C))) \)
\( 0=(A \wedge 13) \wedge(1 A \cup>(13 \vee C)) \)
\( =(A \cap 1)) \wedge \neg A \cup(\neg / 3 \wedge \cap C) \)
\( \equiv(A \cap 13) \wedge(\neg A V \neg B) \wedge(\neg A \vee \neg C) \)

Answer 1

Ja, ist doch OK,  Und-Verbindung der ersten beiden Klammern

ist immer falsch, also kannst du fortfahren

≡ 0 ∧ (¬A ∨ ¬C) 

UNd- Verbindung mit 0 ist immer falsch ! q.e.d.