Hallo,
kannst Du diesen Satz verwenden?
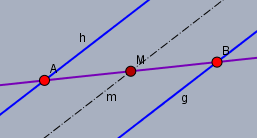
Die Mittelparallele \(m\) eines Parallelenpaars \(h,\,g\) halbiert jede Strecke \(AB\), wobei \(A\) auf \(h\) und \(B\) auf \(g\) liegt.
Dann ginge es z.B. so:
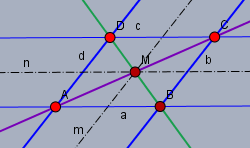
Das Parallelogramm \(ABCD\) wird durch die Parallelpaare \(a,\,c\) und \(b,\,d\) gebildet. Die Mittelparallele von \(a,\,c\) sei \(m\) und die vom Parallelenpaar \(b,\,d\) sei \(n\). Der Schnittpunkt der Mittelparallelen \(m\) und \(n\) sei \(M\).
Die Punkte \(A\) und \(C\) liegen auf beiden Parallelpaaren. Folglich wird die Strecke \(AC\) auch von beiden Mittelparallelen halbiert. Da es nur einen Mittelpunkt von \(AC\) gibt, ist der Mittelpunkt von \(AC\) auch gleichzeitig der Schnittpunkt \(M\) von \(m\) und \(n\).
Die gleiche Überlegung gilt für die Strecke \(BD\). Auch ihr Mittelpunkt muss in \(M\) liegen und fällt folglich mit dem Mittelpunkt von \(AC\) zusammen.
Daraus folgt: der Schnittpunkt der Diagonalen im Parallelogramm halbiert die Diagonalen.
Gruß Werner