Steckbriefaufgabe kubische Funktion

Question

Eine ganzrationalen Funktion 3.ten Grades hat im Punkt P(0|1) die Steigung mp= -1
Ihr Wendepunkt ist W(-1 | 4). Bestimme die Gleichung dieser Funktion und fertige eine Skizze an

Answer 1

Benutze http://www.arndt-bruenner.de/mathe/scripts/steckbrief.htm zur Hilfe und Selbstkontrolle

Eigenschaften

f(0) = 1
f'(0) = -1
f(-1) = 4
f''(-1) = 0

Gleichungssystem

d = 1
c = -1
-a + b - c + d = 4
-6a + 2b = 0

Funktion

f(x) = x^3 + 3·x^2 - x + 1

Skizze

~plot~ x^3+3x^2-x+1;[[-8|8|-2|10]] ~plot~

Comments

Könntest du vielleicht nochmal genauer erklären wie du a und b herausgefunden hast?

Answer 2

Hallo,

eine ganzrationale Funktion 3. Grades und ihre ersten beiden Ableitungen kannst du so darstellen:

\(f(x)=ax^3+bx^2+cx+d\\ f'(x)=3ax^2+2bx+c\\ f''(x)=6ax+2b\)

Um das in der Aufgabenstellung angesprochene Gleichungssystem zu erhalten, "übersetzt" du die gegebenen Informationen:

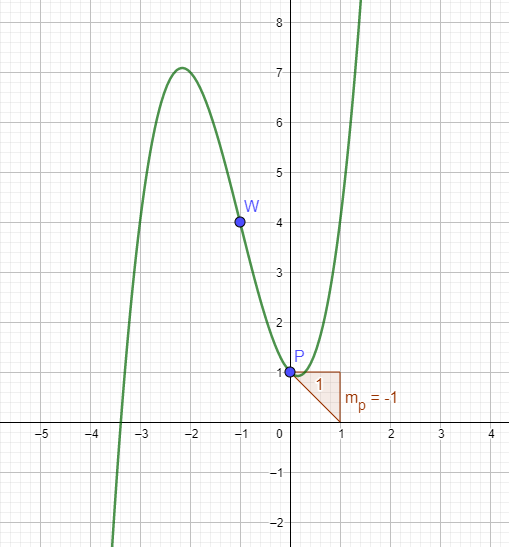
\(P(0|1)\Rightarrow f(0)=1\Rightarrow d=1\\\)

Steigung = Ableitung in diesem Punkt = -1

\(f'(0)=-1\Rightarrow c=-1\)

Ihr Wendepunkt ist W(-1 | 4)

Hieraus ergeben sich die beiden Bedingungen

\(f(-1)=4\Rightarrow -a+b+1+1=4\quad -a+b=2\\ f''(-1)=0\Rightarrow -6a+2b=0\)

Den Rest schaffst du sicher alleine, sonst frage nach.

Gruß, Silvia

Comments

Danke, aber das alles habe ich schon. Ich verstehe nur nicht, wie man auf a und b kommt.

---

\(-a+b=2\Rightarrow b=2+a\)

Einsetzungsverfahren, 2 + a fü b in die andere Gleichung einsetzen ergibt

\(-6a+2(2+a)=0\\ -6a+4+2a=0\\ -4a=-4\\ a=1\\b=2+1=3 \)

---

Hallo Silvia,

Ich hätte eine Frage zu den randwerten könntest du mir erklären wie man diese ermittelt?

---

Hallo Looolo,

dazu empfehle ich dir zwei Videos: