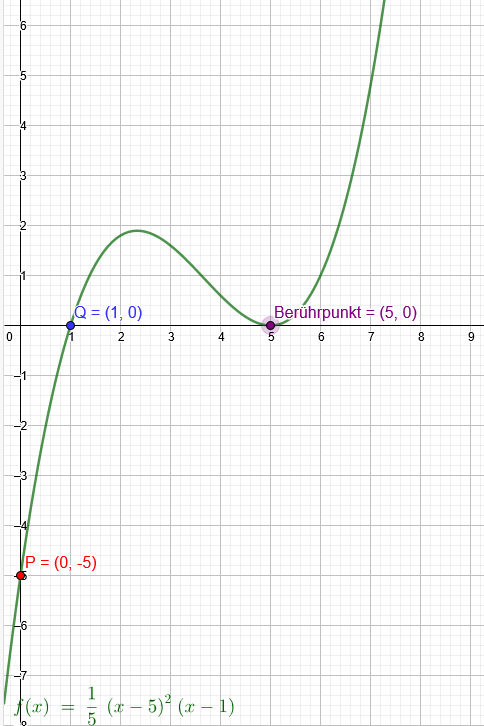
"Bestimme die ganzrationale Funktion 3. Grades, deren Graph durch die Punkte \( P(0 \mid-5) \) und \( Q(1 \mid 0) \) verläuft und die x-Achse bei \( x_{0}=5 \) berührt."
Weg über die Nullstellenform der kubischen Parabel:
\(f(x)=a*(x-5)^2*(x-1)\)
\(P(0|-5)\)
\(f(0)=a*(0-5)^2*(0-1)=-25a\)
\(-25a=-5→a=\frac{1}{5}\)
\(f(x)=\frac{1}{5}*(x-5)^2*(x-1)\)