quadratische Gleichung allgemein:
f(x) = ax2 + bx + c
Wir haben gegeben:
f(-1) = 0 = a*(-1)2 + b*(-1) + c = a - b + c
f(1) = 0 = a + b + c
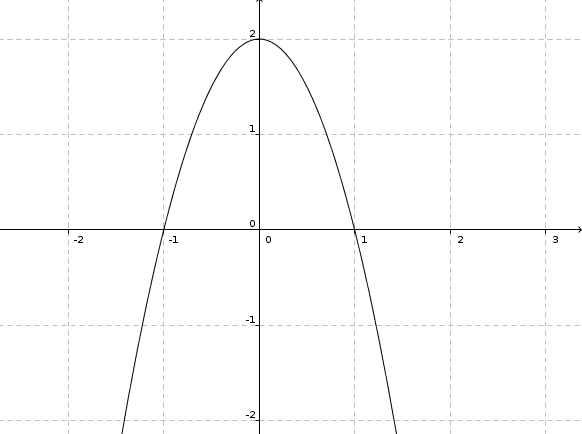
Scheitelpunkt S(0|2), also
f(0) = 2 = a*02 + b*0 + c | c = 2
Es bleiben 2 Gleichungen mit 2 Unbekannten:
a - b + 2 = 0 | a - b = -2
a + b + 2 = 0 | a + b = -2
Addieren wir diese beiden Gleichungen, so ergibt sich
2a = -4
a = -2
b = 0
Die Funktionsgleichung lautet damit:
f(x) = -2x2 + 2
Besten Gruß