Aufgabe: Schwerpunkt im Dreieck- Vektorrechnung
Text erkannt:
11
a) \( \quad \vec{S}=\vec{A}+\frac{1}{2}(\vec{B}-\vec{A})+\frac{1}{3}\left(c-\mu_{i}\right) \)
\( \begin{array}{c} M_{C}=A+\frac{1}{2}(B-A) \\ \vec{S}=\vec{A}+\frac{1}{2}(B-A)+\frac{1}{3}\left(C-\left[A+\frac{1}{2}(B-A]\right)\right. \\ =A+\frac{1}{2} B-\frac{1}{2} A+\frac{1}{3} C-\frac{1}{3} A-\frac{1}{C} D+\frac{1}{6} A \\ -\frac{1}{1} A+\frac{1}{3} A+\frac{1}{2} C \\ \vec{S}=\frac{1}{3}(A+B+C) \end{array} \)
Die Verbindungsstrecke einer Ecke eines Dreiecks mit dem Mittelounkt der gegen-
überliegenden Seite heißt Seitenhalbierende. Die drei Seitenhalbierenden s,, S, und
S, eines Dreiecks ABC schneiden sich in einem Punkt S,
dem Schwerpunkt. Der Schwerpunkt S teilt die Seiten-
halbierenden im Verhältnis 2:1. D.h.: Die Strecke vom
Schwerpunkt bis zum Eckpunkt ist doppelt so lang wie
die Strecke vom Schwerpunkt bis zum Seitenmittel-
punkt.
a) Rechts ist ein Dreieck ABC mit dem Schwer-
punkt S abgebildet. Drücke den Orts-
Me
vektor S des Schwerpunkts mithilfe einer
Vektorkette durch À, B und C aus.
b) Folgere daraus: S = ; (À + B + C). Fasse das Ergebnis in Worte.
c) A (3)-2|1), B(-2|4|2) und C(2|1|3) sind die Eckpunkte eines
Dreiecks. Berechne die Koordinaten seines Schwerpunkts S.
d) Gib die Eckpunkte eines Dreiecks mit dem Schwerpunkt S(- 1|2| -3) an.
Text erkannt:
(ㄱ) (1) Der Schwerpunkt eines Dreiecks
Die Verbindungsstrecke einer Ecke eines Dreiecks mit dem Mittelpunkt der gegenüberliegenden Seite heiBt Seitenhalbierende. Die drei Seitenhalbierenden \( s_{2}, s_{2} \) und \( \mathrm{s}_{\mathrm{c}} \) eines Dreiecks \( \mathrm{ABC} \) schneiden sich in einem Punkt \( \mathrm{S} \), dem Schwerpunkt. Der Schwerpunkt \( S \) teilt die Seitenhalbierenden im Verhältnis \( 2: 1 \). D. h.: Die Strecke vom Schwerpunkt bis zum Eckpunkt ist doppelt so lang wie die Strecke vom Schwerpunkt bis zum Seitenmittelpunkt.
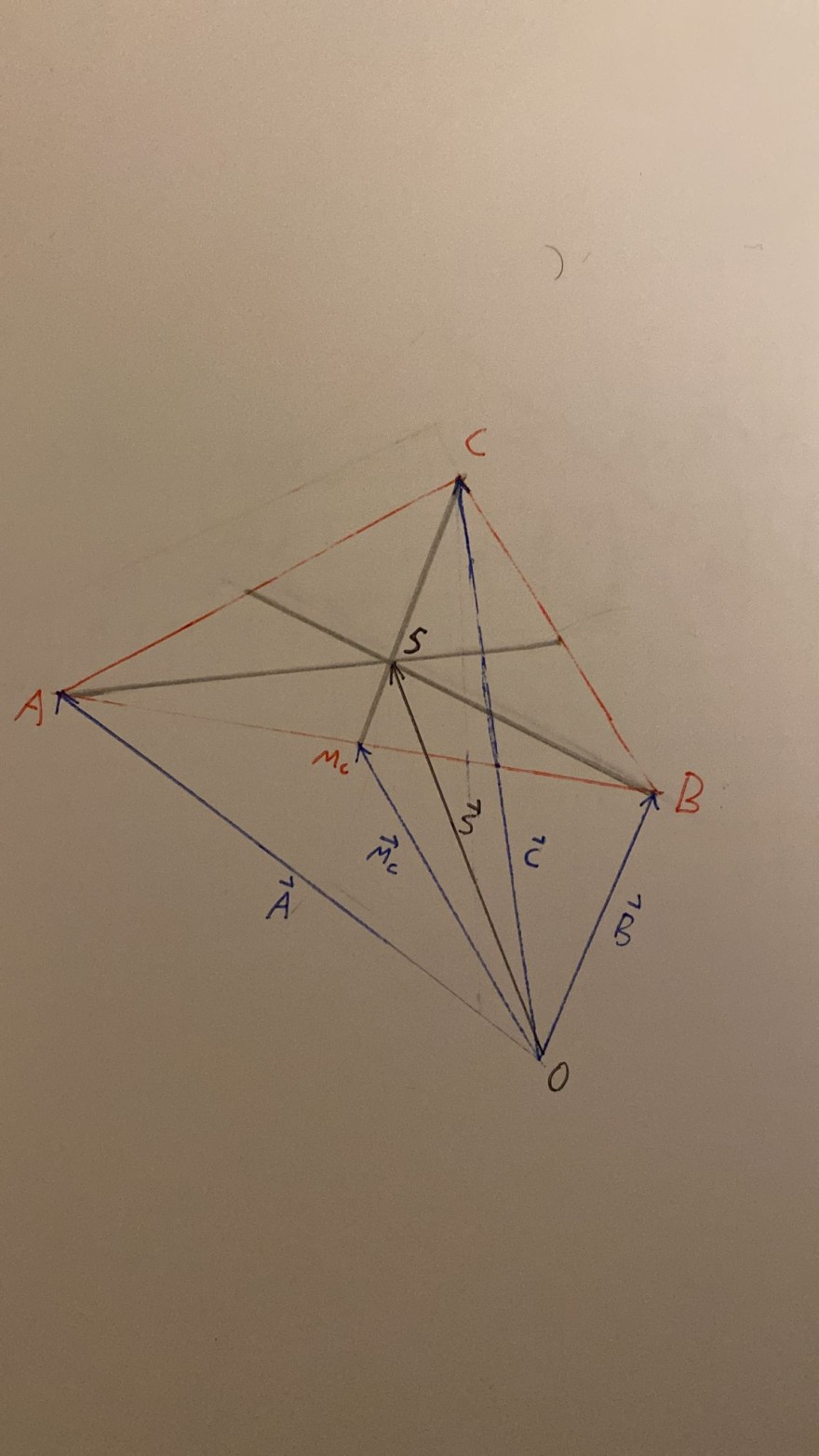
a) Rechts ist ein Dreieck ABC mit dem Schwerpunkt S abgebildet. Drücke den Ortsvektor \( \vec{S} \) des Schwerpunkts mithilfe einer Vektorkette durch \( \vec{A}, \vec{B} \) und \( \vec{C} \) aus.
b) Folgere daraus: \( \vec{S}=\frac{1}{3}(\vec{A}+\vec{B}+\vec{C}) \). Fasse das Ergebnis in Worte.
c) \( A(3|-2| 1), B(-2|4| 2) \) und \( C(2|1| 3) \) sind die Eckpunkte eines Dreiecks. Berechne die Koordinaten seines Schwerpunkts S.
d) Gib die Eckpunkte eines Dreiecks mit dem Schwerpunkt \( S(-1|2|-3) \) an.
Problem/Ansatz:
Ich habe bereits einen Ansatz für die a, bin mir aber nicht sicher ob dieser richtig ist (ich habe hier keine Pfeile über die Vektoren geschrieben):
S=A+1/2(B-A)+1/3(C-Mc)
Mc=A+1/2(B-A)
S=A+1/2(B-A)+1/3(C-(A+1/2(B-A))
=A+1/2B-1/2A+1/3C-1/3A-1/6B+1/6A
=1/3A+1/3B+1/3C
S=1/3(A+B+C)
Zudem wäre es super, wenn mir jemand die anderen Aufgaben auch noch einmal verständlich erklären könnte
(Anbei eine Skizze des Dreiecks wie sie im Buch steht)