Differenzierbarkeit: Zeitaufwand minimieren

Question

Aufgabe: Oberhalb der Gerade g fährt ein Auto mit der Geschwindigkeit v_1 und unterhalb der Geraden g mit der Geschwindigkeit v_2.

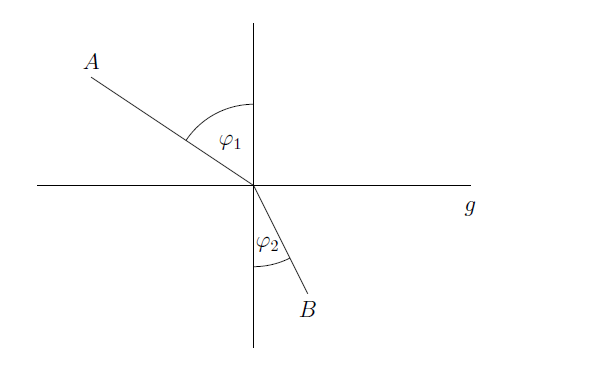
Zeige: Der Zeitaufwand der Strecke im folgenden Bild ist minimal, wenn v_1*sin(φ_2)=v_2*sin(φ_1)

Problem/Ansatz:

Ich habe schon ganz schön viel probiert. Meine zwei besten Ansätze, die aber beide nicht geklappt haben, waren diese:

1. Die Strecke versucht vektoriell aufzuschreiben und dann abzuleiten, da ja der Zeitaufwand minimal wird, wenn die Strecke minimal wird. Also:

s = (\( \begin{pmatrix} v_1*cos(180°-φ_1)\\v_1*sin(180°-φ_1) \end{pmatrix} \) * t + (\( \begin{pmatrix} v_2*cos(180°-φ_2)\\v_2*sin(180°-φ_2) \end{pmatrix} \) * t

Nach Ableiten und Umformen komme ich auf v_1=-v_2. Einsetzen in s ergibt:

s=v_1*t + v_1 * \( \sqrt{-cos(2φ_2} \)  * t

Hilft mir aber irgendwie nicht weiter.

2. Da ich weiß, dass die Geschwindigkeit die Fläche unter der Strecke ist und die Zeit minimal ist, wenn die Geschwindigkeit maximal wird, habe ich versucht die Fläche aufzustellen:

A=1/2 * a_x * a_y + 1/2 * b_x * b_y, wobei a_, b_ jeweils die Koordinaten in x- bzw. y-Richtung der Dreiecke sind. Aber da ich zu wenig Informationen habe, was a_x und a_y sein soll, hilft mir das auch nicht weiter.

Irgendjemand eine Idee? :)

(Tipp: Ist eine Aufgabe im Zuge eines Analysis Kurses über Differenzierbarkeit, also sollte wohl keine großen physikalischen Grundkenntnisse erfordern und irgendetwas mit Ableiten zu tun haben.)

Comments

Eine Möglichkeit wäre das so anzugehen:

---

Was ist bekannt / fest
Strecke A bis Mittelpunkt
Strecke B bis Mittelpunkt

va , vb,
Winkel a , Winkel B

???

---

Hallo

Mir ist die Aufgabe schleierhaft: "Oberhalb der Gerade g fährt ein Auto-- oberhalb sind unendlich viele Richtungen?

2. Der Zeitaufwand der Strecke? welcher Strecke?  in x Richtung? in y Richtung?  aber da 2 Autos fahren kann sich ja nur ihr Abstand ändern?

dein Versuch scheint  s als Abstand der 2 Autos zu sehen ?

dann müsste es aber wohl |s| sein

3.“ Zeitaufwand der Strecke" ist kein verständliches Deutsch

kann gemeint sein  die Zeit für jeweils einen gegebenen Abstand soll minimal sein.

dann musst du ja t(s) differenzieren um ein Max zu finden

ist der Text Original oder deine Interpretation= dann bitte den Originaltext,

lul

---

@ lul: Die Beschreibung

"Oberhalb der Gerade g fährt ein Auto..." usw.

steht in Zusammenhang mit der Skizze.

Wird die bei dir nicht angezeigt?

Der Sachverhalt ist glasklar.

aber da 2 Autos fahren

Nein, es fährt ein Auto von A nach B.

Answer 1

Aloha :)

Willkommen in der Mathelounge... \o/

Startpunkt \(A(x_A|y_A)\) und Endpunkt \(B(x_B|y_B)\) sowie die Beträge der Geschwindigkeiten \(v_1\) und \(v_2\) sind uns vorgegeben. Wir suchen den Punkt \(X(x|0)\) mit \(x\in(x_A|x_B)\) auf der Geraden \(g\), wo der Fahrer die Geschwindigkeit wechseln muss, um möglichst schnell von \(A\) nach \(B\) zu gelangen.

Zu diesem Zweck drücken wir die Gesamtzeit \(t\) in Abhängigkeit von \(x\) aus:

$$t(x)=\frac{\overline{XA}}{v_1}+\frac{\overline{XB}}{v_2}=\frac{\left\|\binom{x_A}{y_A}-\binom{x}{0}\right\|}{v_1}+\frac{\left\|\binom{x_B}{y_B}-\binom{x}{0}\right\|}{v_1}=\frac{\left\|\binom{x_A-x}{y_A}\right\|}{v_1}+\frac{\left\|\binom{x_B-x}{y_B}\right\|}{v_1}$$$$\phantom{t(x)}=\frac{\sqrt{(x_A-x)^2+y_A^2}}{v_1}+\frac{\sqrt{(x_B-x)^2+y_B^2}}{v_2}$$

Im Extremum muss die Ableitung \(t'(x)\) verschwinden:$$0\stackrel!=t'(x)=\frac{-2(x_A-x)}{2v_1\sqrt{(x_A-x)^2+y_A^2}}+\frac{-2(x_B-x)}{2v_2\sqrt{(x_B-x)^2+y_B^2}}=-\frac{x_A-x}{v_1\cdot\overline{XA}}-\frac{x_B-x}{v_2\cdot\overline{XB}}$$

Ein Blick auf deine Skizze offenbart, dass \((x_A-x)=-\overline{XA}\cdot\sin\varphi_1\) ist (das negative Vorzeichen rechts folgt, weil \(x_A<x\) gilt) und dass \((x_B-x)=\overline{XB}\cdot\sin\varphi_2\) ist:

$$0=\frac{\overline{XA}\cdot\sin\varphi_1}{v_1\cdot\overline{XA}}-\frac{\overline{XB}\cdot\sin\varphi_2}{v_2\cdot\overline{XB}}=\frac{1}{v_1}\,\sin\varphi_1-\frac{1}{v_2}\,\sin\varphi_2$$Multiplizieren wir die Gleichung noch mit \(v_1\cdot v_2\) und stellen leicht um, folgt:$$v_2\sin\varphi_1=v_1\sin\varphi_2$$

Answer 2

Hallo,

das entspricht dem Brechungsgesetz für Licht bei der Brechung.

Guck mal hier:

https://de.m.wikipedia.org/wiki/Fermatsches_Prinzip

:-)