Körper mit Punkten A-H Vektoren

Question

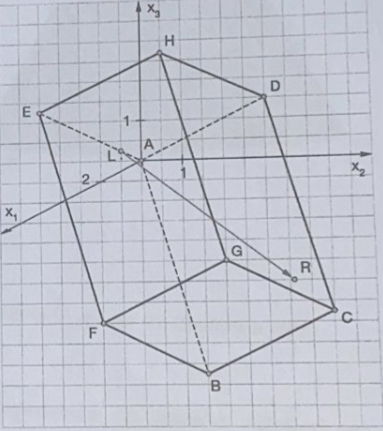
Aufgabe:

Folgender Körper (s. Anhang) mit folgenden Punkten sind gegeben:

A: 0/0/0

B: 9/6/-3

C: 11/10/-1

D: 2/4/2

E: 7/1/3

A,B,C,D bilden Grundfläche und EFGH die deckfläche, die ist parallel kongruent zur Grundfläche.

1.Geben sie die ebene für die deckläche an.

2. Ein Lichtstrahl trifft auf die Grundfläche im Punkt L(11/5/3) und verläuft innerhalb des Körpers in Richtung des Vektors (-11/15/19).

Zeige dass der Lichtstrahl die Grundfläche trifft und berechnen sie die auftreffpunkt.

Problem/Ansatz:

Ich habe erstmal versucht F,G, H zu bestimmen. Aber mir fällt das irgendwie schwer..

F: 7/1/-3

G 11/6/-1

H: 7/4/3

Dann würde ich anschließend für die Bestimmung der ebenengleichubg

E als Stützpunkt wählen und F und G von E subtrahieren um 2 richtungsvektoren zu erhalten.

Vielen dank

Comments

L = E + 1/3 AB + 1/2 AD ??

---

Ein Lichtstrahl trifft auf die Grundfläche im Punkt L(11/5/3)

Auf der Grundfläche ABCD gibt es nur einen einzigen Punkt mit der x-Koordinate 11 - das ist
C(11|10|-1)

Answer 1

Ich habe erstmal versucht F,G, H zu bestimmen. Aber mir fällt das irgendwie schwer..

Es steht doch nirgends, dass du dies tun sollst. Aber es gilt

F = E + AB = [16, 7, 0]
G = E + AB + AD = [18, 11, 2]
H = E + AD = [9, 5, 5]

Zumindest wenn ich mich nicht verrechnet habe

1.Geben sie die ebene für die deckläche an.

E_D: X = E + r·AB + s·AD = [7, 1, 3] + r·[9, 6, -3] + s·[2, 4, 2]

Comments

Dnake für die hilfe!!

Frage zu 2.

Ist L mein stützvektor und v mein richtungsvektor?

Muss ich dann schauen ob diese gerade die grundfläche schneidet? Also ebeneglechung für Grundfläche aufstellen.

Danke!!

---

Genau. Achte aber darauf, das du vermutlich den Richtungsvektor oben falsch hingeschrieben hast.

[0, 0, 0] + r·[9, 6, -3] + s·[2, 4, 2] = [11, 5, 3] + t·[-11, 15, -19] --> r = 0.8 ∧ s = 0.8 ∧ t = 0.2

So macht das deutlich mehr Sinn.

Answer 2

Die Vektoren AE, BF, CG und DH sind die Gleichen - jeweils \(\overrightarrow{AE}= \begin{pmatrix} 7\\1\\3 \end{pmatrix} \) .

Kontrolliere, ob mit deinen Punkten BF, CG und DH diese Forderung erfüllen, und korrigiere gegebenenfalls.