Differenzierbarkeit/ stetigkeit einer Funktion

Question

Aufgabe:

Stetigkeit/ Differenzierbarkeit der folgenden Funktionen

Problem/Ansatz:

f1(x)=|x| mit IR→IR

f2(x)=|x| mit ]-Unendlich,0]

Wegen Stetigkeit: beide Funktionen sind stetig, denn zB. lim_(x→0)|x|= 0 =f(0).

Wegen Differenzierbarkeit:

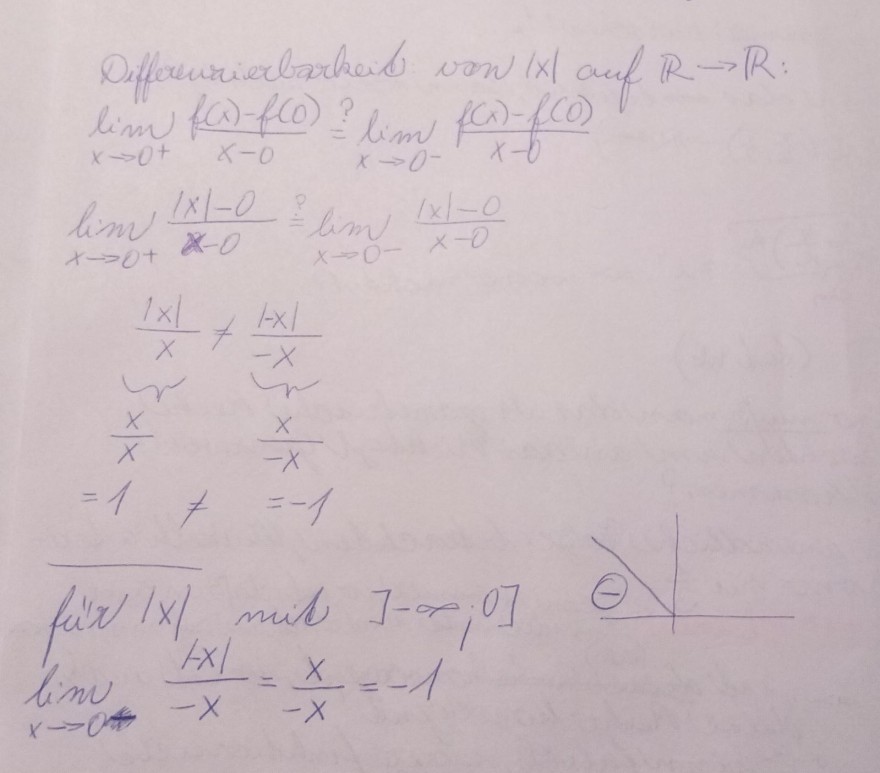
Bei dem zweiten Fall (für |x| mit ]-Unendlich,0]): man kann sich nur aus einer Seite annähern, da die Definitionsmenge nur für 0 aus den negativen Richtung ,,definiert,, ist. Deswegen würde man die lim aus der anderen Richtung nicht brauchen.

Ist das richtig?

Danke!

Answer 1

Hier der Graph

Der Graph zeigt an das
Stetigkeit gegeben ist.
Im Punkt x = 0 welchselt die Steigung von -1 auf 1.
Die Funktion ist nicht differenzierbar.

Ist der Def-Bereich eingeschränkt auf - unendlich bis 0
( nur der linke Teil ) dan ist die Funktion stetig und auch
differenzierbar. Die Steigung ist nur -1.

mfg