Wie bekomme ich diese Wurzelgleichung in eine gescheite Kostenfunktion (Extremwertaufgabe)?

Question

Aufgabe:

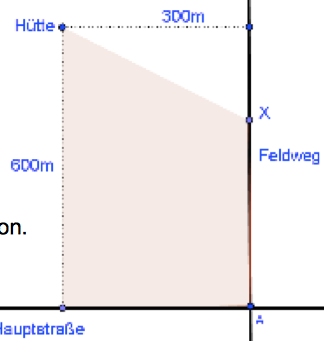
Herr Maier besitzt eine Hütte, 600m von der Hauptstraße und 300m von einem zur Straße normal verlaufenden Feldweg entfernt.
Er möchte mit Kabelfernsehen versorgt werden.
Die Verlegungskosten werden ab dem Verteilerpunkt A verrechnet. Entlang des Feldweges kostet die Verlegung von 1m Kabel €100. Querfeldein durch das Grundstück von Herrn Maier das Doppelte davon.

Aufgabenstellung:
a) Stelle die Zielfunktion auf, um die kostengünstigste Variante der Verlegung zu berechnen.
Ermittle die Länge der Strecke AX für diese kostengünstigste Variante!

Problem/Ansatz:

Also ich hab mal so gerechnet:

K(x) = 100*d + 200*Wurzel((600-d)^2+300^2))

(entschuldigt diese Darstellung, aber irgendwie versteh ich nicht wie ich hier die mathematischen Zeichen eingeben soll)...

aber muss ich ja dann vereinfachen, damit ich aus der 1.Ableitung die kostengünstigste Variante bekomme... Und genau das krieg ich einfach nicht gebacken, es sollte für d = 426,8 rauskommen, keine Chance.. Wo hab ich bloss den Wurm??

Zum besseren Verständnis - d ist die Länge AX und dann kommt der Weg von X zu H.

Ich danke herzlich für alle Hinweise...

Answer 1

Das x ist ja dann das d

K(d) = 100*d + 200*Wurzel((600-d)²+300²)

==>  K ' (d) = 100 + 200 * 1 / ( 2* Wurzel((600-d)²+300²))

               = 100 + ( 200(d-600)) / √(d^2 -1200d +450000)

Das gleich 0 gibt

( 200(d-600)) / √(d^2 -1200d +450000) = -100

200(d-600) = -100*√(d^2 -1200d +450000)    :100

2d-1200 = √(d^2 -1200d +450000)    quadrieren

4d^2 - 4800d + 1440000=d^2 -1200d +450000

3d^2 - 3600d + 990000 = 0   | :3

d^2 - 1200d +330000 = 0

pq-Formel liefert 2 Lösungen. Die richtige ist 426,8

Comments

Wow - danke! Jetzt weiß ich was mein Denkfehler war - ich dachte ich muss die normale Formel gleich umformen, nicht die Ableitung!! *Hirnklatsch*

Aber: bei der Ableitung bin ich jetzt etwas ratlos - wie kommst du auf 200*1/2*wurzel(…..) und dann auf (200(d-600))/….???

---

Ahhhhh, das erste fällt mir grad ein - die Ableitung einer Wurzel ist auf 1/2 , oder?? *nachdenk* aber warum dann die Wurzel im Nenner?

Seufz…

Danke für die Geduld %-)

---

Ich bin wirklich doof - ich hab nicht an die Kettenregel gedacht…

Danke für die Erklärung!!!!!!