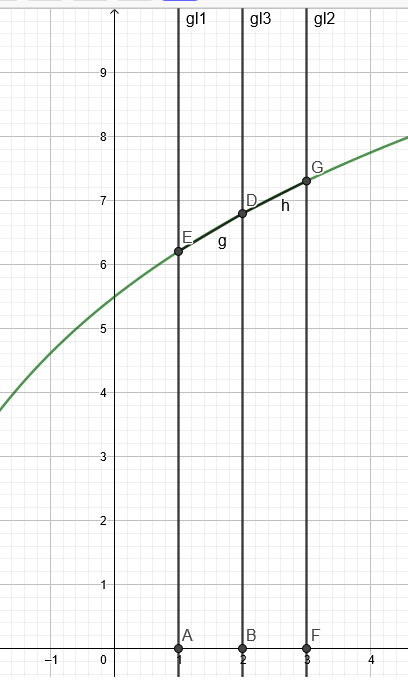
f(x)=C*ln(4,6+x)
Gerade x=1 schneidet f(x) in f(1)=C*ln(4,6+1)=C*ln(5,6) Strecke AE: C*ln(5,6)
Gerade x=2 schneidet f(x) in f(2)=C*ln(4,6+2)=C*ln(6,6) Strecke BD: C*ln(6,6)
Gerade x=3 schneidet f(x) in f(3)=C*ln(4,6+3)=C*ln(7,6) Strecke FG: C*ln(7,6)
Fläche des Trapez ABDE:
A₁=\( \frac{C*ln(6,6)+C*ln(5,6)}{2} \)*1
Fläche des Trapez BFGD:
A₂=\( \frac{C*ln(7,6)+C*ln(6,6)}{2} \)*1
A=A₁+A₂
162=\( \frac{C*ln(6,6)+C*ln(5,6)}{2} \)+\( \frac{C*ln(7,6)+C*ln(6,6)}{2} \)
162=\( \frac{C}{2} \)*[ln(6,6)+ln(5,6)+ln(7,6)+ln(6,6)] C=...