Analytische geometrie punkt ebene verschiebung

Question

Aufgabe:

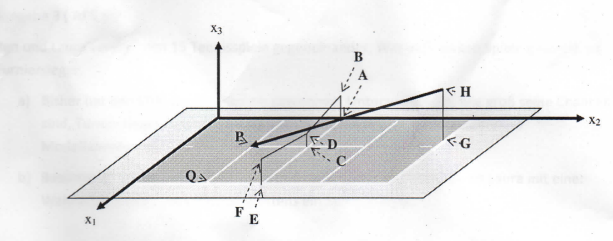
Die Abbildung stellt in einem dreidimensionalen Koordinatensystem schematisch das Spielfeld (Einzelfeld) eines Tennisplatzes dar. Das Feld wird in der Mitte durch ein Netz unterteilt, das von den Außenpfosten AB und EF gehalten wird. Die Netzoberkante ist in der Mitte im Punkt D niedriger als außen in den Punkten B und F, aber ansonsten geradlinig gespannt. Die angegebenen Maße des Platzes sind aus Vereinfachungsgründen auf ganze Meter gerundet. Auch die Koordinaten der unten Angegebenen Punkte sind in Metern zu verstehen.
Die Bälle fliegen in diesem Modell geradlinig, es sollen jegliche Spins vernachlässigt werden. Außerdem wird der Tennisball als Punkt aufgefasst.
Die angegebenen Punkte des Tennisfelds haben die folgenden Koordinaten:
A(0|12|0) B(0|12|1,1) C(4,5|12|0) D(4,5|12|0,9) E(9|12|0) F(9|12|1,1) P(4,5|6|0) Q(9|6|0)
Im Punkt (4|24|0) steht der Aufschläger, der versucht den Tennisball vom Punkt H(4|24|3) seines Schlägers aus geradlinig in den Eckpunkt P des gegnerischen Aufschlagfeldes ECPQ zu schlagen.
Dem Aufschläger gelingt es, seinen Aufschlag genau in dem Punkt P zu platzieren. Von dort aus springt der Ball idealtypisch, wie in der Abbildung 2 dargestellt wird, ab in Richtung des Gegners, der auf der Grundlinie (der x1-Achse) steht.

Dem Spieler gelingt es nicht jedes mal den Punkt P zu treffen. Oft sind abweichungen bis zu 0.5m realistisch. Bestimmen sie nun diejenigen punkte in der x^1 x² ebene indem der schläger des gegners zum return trifft.

…

Problem/Ansatz:

Bis zu 0.5m radius abweichung vom Punkt p resultiert doch in unendlich viele verschiedene Punkte in der x^1x² ebene. Was genau soll ich denn da berechnen? Oder wieviele punkte?

Answer 1

Der mögliche Auftreffbereich des Aufschlags ist ein Kreis mit dem Radius 0,5 m.

Ich vermute, dass der Ankommensbereich in der x1-x3-Ebene ebenfalls ein Kreis oder wenigstens eine Ellipse ist.

Berechne also, wie die Punkte des Kreises nach der Reflexion in die x1-x3-Ebene abgebildet werden.

Comments

Ich habe keine Ahnung wie das geht.

Answer 2

Wir hatten die Fragen irgend wann schon mal:

Eine Abweichung von Zielpunkt P ist ein Kreis r=0.5 in z=0 - so weit so gut, aber was soll mir

>Bestimmen sie nun diejenigen punkte in der x1 x² ebene indem der schläger des gegners zum return trifft. <

sagen? Ist das originaltext?

Nach meinem Rechengang war   der Returnierpunkt R nach Absprung von P gesucht.

Comments

Jaa das ist Originaltext. Darum verwirrt mich das weil das ergebnis eine fläche in der x1x3 darstellt. Aber wie ich dessen firm und grenzen berechnen soll wüsste ich auch nicht. Das ist eine GK Aufgabe und das wirkt auf mich eher wie ein fehler in der aufgabenstellung.

Wie könnte ich die fläche in der x1x3 ebene berechnen damit ich irgendwas da stehen habe?

---

Das kann nicht der Originaltext sein, weil die Aussage dummes Zeug fabuliert.

Der Rückschlag wird in der x1x3-Ebene angenommen, das ist der Punkt R.

In der x1x2-Ebene springt der Ball im Punkt P, bzw im Kreis drumrum, auf ...

ADD Fundstück: Vorgänger unter

https://www.mathelounge.de/848161/tennisplatztextaufgabe-analytische-geomeotrie

---

Ich habe die Aufgabe im internet gefunden. Diese Teilaufgabe kommt darin nicht vor. Vielleicht hat meine Lehrerin die hinzugefügt und etwas falsch gemacht

---

Die Aufgabenstellung geht davon aus, dass der Ball in dem Kreis um P (x3,z=0) aufdotzt und im Rückschlag bei x2,y=0 angenommen wird.

Wenn statt einem Absprung-Punkt ein Absprung-Kreis angenommen wird, dann ist statt einem Retunierpunkt R eine Ellipse zu erwarten, etwa

Statt P ein Kreis

\(k(t)=P + 0.5 \; \left(\begin{array}{r}\operatorname{cos} \left( t \right)\\\operatorname{sin} \left( t \right)\\0\\\end{array}\right)\)

und in einer Abpraller-Geraden

\(g(k):=P + k \; \left(\begin{array}{rrr}1&0&0\\0&1&0\\0&0&-1\\\end{array}\right) \; \left(P - H \right) \)

wäre P durch k(t) zu ersetzen und bei y(g(k))=0 zurückzuschlagen.