Aufgabe
Text erkannt:
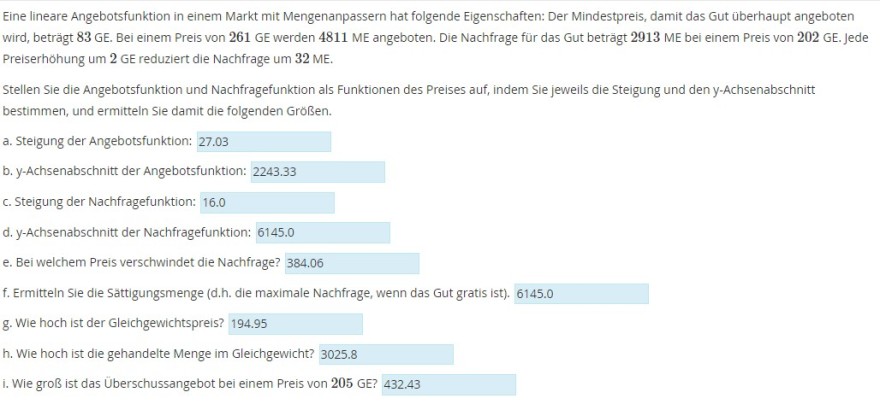
Eine lineare Angebotsfunktion in einem Markt mit Mengenanpassern hat folgende Eigenschaften: Der Mindestpreis, damit das Gut überhaupt angeboten wird, beträgt \( 83 \mathrm{GE} \). Bei einem Preis von 261 GE werden 4811 ME angeboten. Die Nachfrage für das Gut beträgt 2913 ME bei einem Preis von 202 GE. Jede Preiserhöhung um 2 GE reduziert die Nachfrage um \( 32 \mathrm{ME} \).
Stellen Sie die Angebotsfunktion und Nachfragefunktion als Funktionen des Preises auf, indem Sie jeweils die Steigung und den y-Achsenabschnitt bestimmen, und ermitteln Sie damit die folgenden Grơßen.
a. Steigung der Angebotsfunktion: \( 27.03 \)
b. \( y \)-Achsenabschnitt der Angebotsfunktion: \( 2243.33 \)
c. Steigung der Nachfragefunktion: \( 16.0 \)
d. \( y \)-Achsenabschnitt der Nachfragefunktion: \( 6145.0 \)
e. Bei welchem Preis verschwindet die Nachfrage? \( 384.06 \)
f. Ermitteln Sie die Sattigungsmenge (d.h. die maximale Nachfrage, wenn das Gut gratis ist). \( 6145.0 \)
g. Wie hoch ist der Gleichgewichtspreis? \( 194.95 \)
h. Wie hoch ist die gehandelte Menge im Gleichgewicht? \( 3025.8 \)
i. Wie groß ist das Überschussangebot bei einem Preis von 205 GE? \( 432.43 \)
Problem/Ansatz:
Ich habe die Aufgabe bereits gerechnet, leider haben sich zwei Fehler eingeschlichen auf die ich nicht draufkomme… Würd mich sehr freuen, wenn mir wer helfen kann.
LG :)
\( \begin{array}{l} s(83)=83 b-\beta=0 \\ s(261)=261 b-\beta=4811 \\ 4811=261 b-\beta \\ \frac{-O}{4811}=83 b-\beta \\ \Rightarrow b=27,02809=27,03 \\ b=3811=261 \cdot 27,02809-\beta \\ 4811=7054,33149-\beta \\ \beta=2243,33149 . \end{array} \)
d. h. Achsenabsabruill ist \( -2243,33149 \), wenn rach \( \beta \) gehagl wild positiv
\( \begin{aligned} D(202) &=-202 \cdot 2+\alpha=2913 \\ D(204) &=-204 \cdot 2+\alpha=2881 \\ \frac{2913}{-2881} &=-202 a+\alpha \\ 32 &=-204 \cdot a+\alpha \\ 16 &=22 \end{aligned} \)
e) \( D(p)=-32 / 2 \cdot p+6145=0 \)
\( p=\frac{6145}{16}=384,0625=384,06 \)
\( D(0)=-32 / 2 \cdot 0+6145=6145 \cdot \alpha \)
g) \( S(p)=D(p) \)
\( 27,02809 \cdot p-2243,33149=-3212 \cdot p+6145 \)
\( 27,02809 \cdot p+16 p=645+2243,33149 \)
\( 43,02809 \cdot p=8388,33149 \)
\( \begin{aligned} p^{*}=\frac{8388,33149}{43,02809} &=194,95012 \\ &=194,95 \end{aligned} \)
\( \begin{array}{l} S\left(p^{\circ}\right)=D\left(p^{4}\right) \\ D\left(p^{*}\right)=-32 / 2 \cdot 194,95012+6145=3025,79808 \end{array} \)
\( \text { i) } \begin{aligned} S(205) &=205 \cdot 27,02809-2243,33149=3025,8 \\ D(205) &:(-16 \cdot 205)+6145=2865 \end{aligned} \)
\( \begin{aligned} U=& \overbrace{2865}^{D}-\frac{41217837}{12500}=-432,0.2696 \\ \frac{41217837}{12500}-2865 &=432,42696=432,43 \end{aligned} \)