Aufgabe:
Text erkannt:
Aufarbe 2) Fortsetawng vor
A afgae 2) Fortsctzung von Wochcraufgabe Q2-05 (Carportaufgabe)
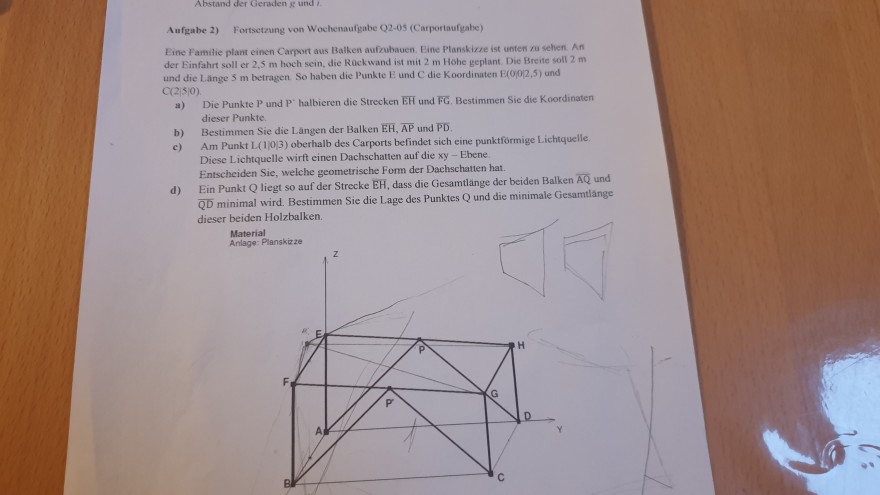
Eine Famthie plant einen Carport aus Balken aufzubauen. Eine Planskirse ist unten ru sehen. An der Finfahrt soll er \( 2,5 \mathrm{~m} \) hoch sein, die Rockwand ist mit \( 2 \mathrm{~m} \) Hobhe geplant. Die Breite soll \( 2 \mathrm{~m} \) und die Lainge \( 5 \mathrm{~m} \) betragen. So haben die Punkte \( \mathrm{E} \) und \( \mathrm{C} \) die Koordinaten \( \mathrm{E}(0,0 \mid 2,5) \) und \( \mathrm{C}(2|5| 0) \).
a) Die Punkte P und \( P^{\prime} \) halbieren die Strecken \( \overline{E H} \) und \( \overline{F G} \). Bestimmen Sie die Koordinaten dieser Punkte.
b) Bestimmen Sie die Làngen der Balken EH, \( \overline{\mathrm{AP}} \) und \( \overline{\mathrm{PD}} \).
c) Am Punkt L(1,0|3) oberhalb des Carports befindet sich eine punktformige Lichtquelle. Diese Lichtquelle wirft einen Dachschatten auf die \( x y \) - Ebene
Entscheiden Sie, welche geometrische Form der Dachschatten hat.
d) Ein Punkt Q liegt so auf der Strecke EH, dass die Gesamtlange der beiden Balken \( \overline{\mathrm{AQ}} \) und \( \overline{Q D} \) minimal wird. Bestimmen Sie die Lage des Punktes \( Q \) und die minimale Giesamtlange dieser beiden Holzbalken.
Material Anlage: Planskiz ze
F
Problem/Ansatz:
Hallo,
ich brauche bei dieser Aufgabe Hilfe.
Ich verstehe das Thema Vektoren nicht so gut. Kann jemand mir bei Aufgabe 2 helfen und ausführlich erklären? Dankeeee sehr