Bestimme die Maße des Spielfeldes mit maximalem Flächeninhalt.

Question

Aufgabe:

Ein Fußballtrainer verwendet 50 m Markierungsband, um damit Spielfelder abzustecken.

a) Der Trainer möchte ein möglichst großes rechteckiges Spielfeld abstecken. Dazu legt er eine Tabelle an. Vervollständige sie.

Länge:             Breite:              Flächeninhalt:

5m                   20m

6m

7m

8m

9m

b) Die Länge des Rechtecks in m sei x. Stelle einen Term für die Breite in m und einen Term für den Flächeninhalt in Quadratmeter auf.

c) Bestimme die Maße des Spielfeldes mit maximalem Flächeninhalt.

Problem/Ansatz:

Wir behandeln zur Zeit das Thema Optimierungsprobleme im Unterricht und ich verstehe gar nichts. Ich weiß nicht, wie man auf die Gleichungen kommen soll und so weiter. Ich würde mich über eine Antwort freuen!

Viele Grüße

Comments

Du schaffst es aber doch bestimmt, die Tabelle zu vervollständigen, oder nicht?

Answer 1

a) Das Markierungsband ist 50m lang.

Umfang vom Rechteck:  Länge (a) +Breite(b)+ Länge(a) +Breite(b)

2a+2b=U   a*b=Fläche(A)

Länge: 5   →  2*5+2*b =50  →  2b= 50-2*5  →2b= 50-10 →b=20   (A) = 5*20=100

Länge: 6 →  2*6+2*b =50  →  2b= 50-2*6 →2b= 50-12 →b=19

(A) = 6*19=114  

Länge: 7  usw

Comments

Danke für die Antwort

---

b) Die Länge des Rechtecks in m sei x. Stelle einen Term für die Breite in m und einen Term für den Flächeninhalt in Quadratmeter auf.

A(x)=x*(25-x)=25x-x^2

c) Bestimme die Maße des Spielfeldes mit maximalem Flächeninhalt.

A(x)=-x^2+25x |*(-1)

-A(x)=x^2-25x  |+quadratische Ergänzung (\( \frac{25}{2} \))^2

-A(x)+12,5^2=x^2-25x+12,5^2

-A(x)+12,5^2=(x-12,5)^2|*(-1)

A(x)-12,5^2=-(x-12,5)^2 |+12,5^2

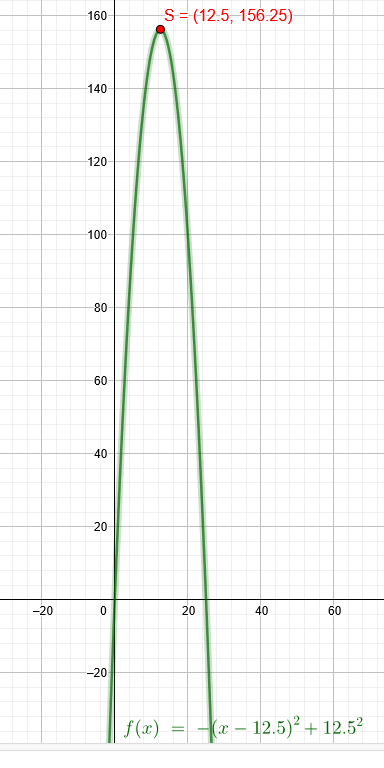
A(x)=-(x-12,5)^2 +12,5^2

Scheitelpunkt S(12,5|156,25)

Die Länge des Spielfelds 12,5m und die Breite auch 12,5m

Die maximale Fläche beträgt 156,25m^2.

Answer 2

Länge:           Breite:             Flächeninhalt:

a                   25-a                  (25-a)·a

Setze für a jeweils die gegebene Länge.

Der größtmögliche Flächeninhalt ergibt sich für die Nullstelle der erste Ableitung von f(a)=(25-a)·a=25a - a² mit f '(a)=25-2a-

0=25-2a hat die Lösung a=12,5. Maximaler Flächeninhalt: 12,5².

Comments

Vielen Dank!