Text erkannt:
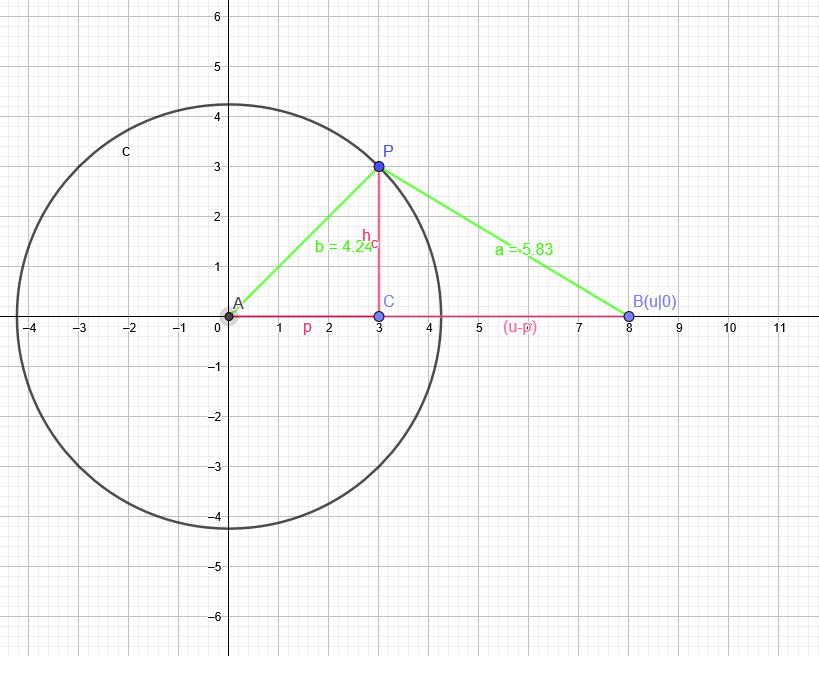
\( A=\frac{u \cdot h_{c}}{2} \) soll maximal werden.
1. \( ) p^{2}+h_{c}^{2}=4,24^{2} \rightarrow h_{c}^{2}=4,24^{2}-p^{2} \in 2 . \).)
2. \( (u-p)^{2}+h_{c}^{2}=5,83^{2} \)
\( (u-p)^{2}+4,24^{2}-p^{2}=5,83^{2} \)
\( u^{2}-2 u p=16,0113 \rightarrow 2 u p=u^{2}-16,0113 \rightarrow p=\frac{u^{2}-16,0113}{2 u} \rightarrow p^{2}=\frac{\left(u^{2}-16,0113\right)^{2}}{4 u^{2}} \)
\( h_{c}^{2}=4,24^{2}-\frac{\left(u^{2}-16,0113\right)^{2}}{4 u^{2}} \rightarrow h_{c}=\sqrt{4,24^{2}-\frac{\left(u^{2}-16,0113\right)^{2}}{4 u^{2}}} \)
\( A(u)=\left.\frac{u}{2} \sqrt{4,24^{2}-\frac{\left(u^{2}-16,0113\right)^{2}}{4 u^{2}}}\right|^{2} \)
\( A^{2}(u)=\frac{u^{2}}{4}\left(4,24^{2}-\frac{\left(u^{2}-16,0113\right)^{2}}{4 u^{2}}\right)=\frac{4,24^{2}}{4} \cdot u^{2}-\frac{1}{16} \cdot\left(u^{2}-16,0113\right)^{2} \)
\( \frac{d A^{2}(u)}{d u}=4,24^{2} \cdot \frac{1}{2} \cdot u-\frac{1}{8} \cdot\left(u^{2}-16,0113\right) \cdot 2 u \)
\( 4,24^{2} \cdot \frac{1}{2} \cdot u-\frac{1}{8} \cdot\left(u^{2}-16,0113\right) \cdot 2 u=0 \)
\( u \cdot\left(4,24^{2} \cdot \frac{1}{2}-\frac{1}{4} \cdot\left(u^{2}-16,0113\right)\right)=0 \)
\( u_{1}=0 \)
\( \left(4,24^{2} \cdot \frac{1}{2}-\frac{1}{4} \cdot\left(u^{2}-16,0113\right)\right)=0 \)
\( u \approx 7,208 \)
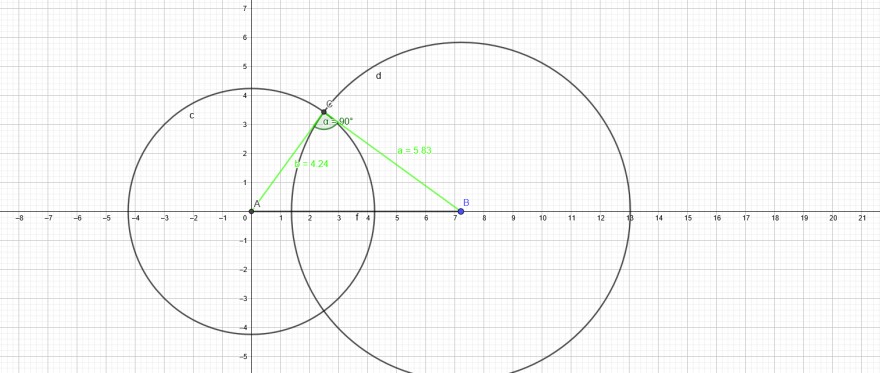
\( a^{2}+b^{2}=u^{2} \ldots . \) mfG Moliets