Integration mittels Substitution einer verketteten e-Funktion

Question

Liebe Forum-Mitglieder,

ich habe eine Frage zu folgendem Integral, welches mittels Substitution gelöst wurde:

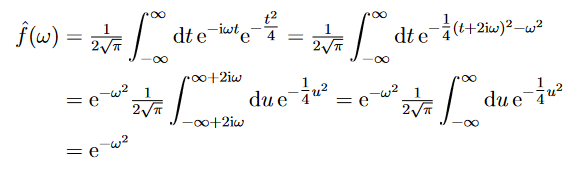
Davon verstehe ich den letzten Schritt nicht. Wie kommt man darauf, dass sich das Integral anscheinend wegkürzt, als dann 2*sqrt(pi) ergeben sollte? Wie rechnet man dieses Integral sauber aus?
Ich würde mich auf jede Hilfe freuen!
Liebe Grüße,

Hybridorbital

Answer 1

Aloha :)

Hier wurde das Gauß-Integral verwendet:$$\int\limits_{-\infty}^\infty e^{-(x+i\cdot a)^2}\,dx=\int\limits_{-\infty}^\infty e^{-x^2}dx=\sqrt{\pi}\quad\text{für alle }a\in\mathbb C$$

Mit der Substitution \(x=\frac t2\) und \(dx=\frac{dt}{2}\) ist dann nämlich:$$\sqrt\pi=\int\limits_{-\infty}^\infty e^{-x^2}\,dx=\int\limits_{-\infty}^\infty e^{-t^2/4}\,\frac{dt}{2}\quad\implies\quad\int\limits_{-\infty}^\infty e^{-t^2/4}dt=2\sqrt\pi$$

Answer 2

Hallo

zu diesem Integral gibt es keine  übliche Stammfunktion,  (die "Stammfunktion ist erf , die "Errorfunktion" sondern man weiss das Ergebnis mit 2*√π

bzw für das Integral über e-t^2 das Ergebnis √π

Gruß lul