Schnittpunkte eines Kreises mit der Mediane berechnen

Question

Aufgabe:

Ermittle die Schnittpunkte des Kreises k mit der 1. Mediane und der 2. Mediane!

k: (x-1)² + (y - 1)² = 8

Problem/Ansatz:

Komme bei diesem Beispiel nicht weiter. Bitte um Hilfe - Danke!

Answer 1

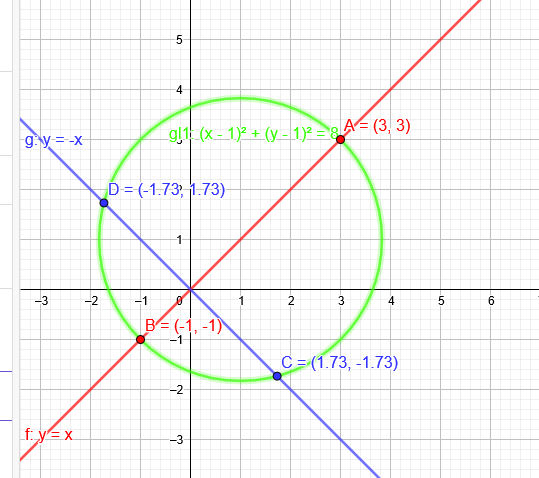
\( (x-1)^{2} + (y-1)^{2} = 8\)

\(y=x\)

\( (x-1)^{2} + (x-1)^{2} = 8\)

\(2* (x-1)^{2} = 8\)

\((x-1)^{2} = 4\)

1.)\((x-1)=2\)

\(x₁=3\)        \(y₁=3\)

2.)\((x-1)=-2\)

\(x₂=-1\)     \(y₂=-1\)

\(y=-x\)

\( (x-1)^{2} + (-x-1)^{2} = 8\)

\( (x-1)^{2} + (x+1)^{2} = 8\)

\( (x^{2}-2x+1) + (x^{2}+2x+1) = 8\)

\(x^{2}=3\)

\(x₁=\sqrt{3}\)       \(y₁=-\sqrt{3}\)

\(x₂=-\sqrt{3}\)      \(y₂=\sqrt{3}\)

Comments

Vielen lieben Dank!

Answer 2

k = 8 ist der Radius ?

1.Mediane
x^2 + y^2 = 8^2
45 °
x^2 + x^2 = 8^2
2x^2 = 64
x = 5.657
y = 5.657

( 5.657 | 5.657 )

2 :Mediane
-45 °
( 5.657 | minus 5.657 )

Comments

Fragesteller :  (x-1)² + (y - 1)² = 8
Du :   x² + y² = 8²

Fällt dir eventuell ein Unterschied auf ?

---

Vielen Dank!

Leider passt das Ergebnis nicht mit dem im Lösungsheft zusammen.

Für die 1. Mediane (3/3) und (-1/-1)

Für die 2. Mediane (Wurzel 3 / - Wurzel 3) und (- Wurzel 3 / Wurzel 3)

Gibt es hier noch einen anderen Lösungsansatz?

---

Ich hatte mein Wissen über Mediane bei
https://www.mathe-lexikon.at/geometrie/kartesisches-koordinatensystem/mediane.html
geholt.
Das stimmten diesem Fall leider nicht.

Wenn ich ganz einfach die Gleichung
(x-1)^2 + (y - 1)^2 = 8
mit y = x
berechne kommt
x= -1
und

x= 3
heraus.

---

Danke für die Bemühungen!!!

Auf diese Lösungen bin ich im Übrigen auch gekommen, aber leider stimmen sie mit dem Lösungsheft nicht überein.

---

( -1 | -1 )
( 3 | 3 )
Für die 1. Mediane stimmt
die Lösung aber.

Sonst mußt du halt einmal fragen
was es mit den 2.Medianen auf
sich hat.