Anordnung von 9 Kreisen mit gleichem Radius.

Question

Ordne 9 Kreise mit gleichem Radius so an, dass zu je zwei Kreisen eine gemeinsame Tangente gehört, die genau einen dritten Kreis berührt.

Answer 1

Hallo Roland,

mein Vorschlag sähe so aus:

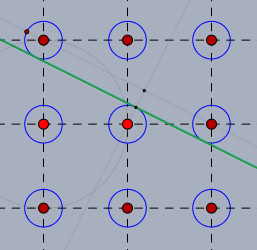
Die horizontalen, vertikalen und diagonalen Tangenten erklären sich von selbst. Und die fehlende Tangente, die jedes Kreistripel im Rösselsprung verbindet, habe ich eingezeichnet.

Die Mittelpunkte der 9 Kreise liegen in einem quadratischem Raster und der Radius \(r\) der Kreise ist$$r = \frac a{10}\sqrt 5 $$wenn \(a\) das Rastermass ist.

Gruß Werner

Answer 2

Das klappt sogar mit 10 Kreisen

Comments

Danke für den Hinweis. Ich hatte ein Wort in der Aufgabenstellung vergessen.

Answer 3

Die Mittelpunkte der 9 Kreise lassen sich auch zu einem regelmäßigen Neuneck anordnen.