Berechne, wie viel Prozent Abfall bei deiner an Anordnung entsteht.

Question

Aufgabe:

Berechnung von einer Verpackung, welches mit 1kg Reis befüllt ist.

Problem/Ansatz:

Es soll eine auffällige und ansprechende Verpackung sein (Die Verpackung muss aus mindestens zwei geometrischen Körpern bestehen von denen mindestens eine pyramidenförmig oder kegelförmig sein muss.) Prüfe, welches Volumen 1 kg Reis hat. Weise durch Berechnungen nach, dass deine Verpackung nach dem Befehl mit 1 kg Reis zwischen 5-15 % Luft enthält.

Fertige 1. eine Zeichnung deiner Verpackung an als zusammenhängendes Körpernetz in Originalgröße und 2. das zusammengeklebte Modell. Nimm an, deine Verpackung soll in großer Stückzahl hergestellt werden. Ordne die Körpernetze deine Verpackung platzsparend auf einem DinA0-Bogen an und übertrage die Umrisse. Berechne, wie viel Prozent Abfall bei deiner an Anordnung entsteht.

Es wäre echt nett wenn mir jemand helfen könnte, bin wirklich am verzweifeln mit dieser Aufgabe.

Lg

Comments

Hallo

diese Aufgabe verlangt von dir doch ein wenig Kreativität und Eigeninitiative.

1. irgendwo das Volumen von 1kg Reis abschätzen ( geht in einen Lebensmittelladen falls ihr keinen Reis zu Hause habt.)

 2. eine eckige oder runde Form erfinden die eine Pyramide oder einen Kegel beinhaltet.

3. die Form so bemaßen, dass sie etwa 10% größer ist als das Volumen aus 1.

Da es ja auf deine Ideen ankommt, ist das keine Aufgabe für Hilfe, entwarf den Körper, dann sag, wo deine Schwierigkeiten liegen.

lul

Answer 1

Google behauptet, 1 dm³ Reis wiege 0,7 kg.

1 kg Reis hat demnach ein Volumen von 1 dm³ / 0,7 ≈ 1,429 dm³, d.h. ein Würfel mit Kantenlänge \( \sqrt[3]{1,429 \, dm^3} \) also 11,262 cm.

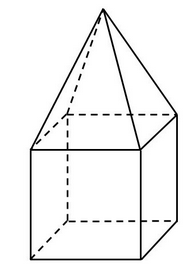
Auf diesen mit Reis gefüllten Würfel setze ich noch eine Pyramide mit 10 % Luftvolumen, d.h. die Pyramide hat ein Volumen von 1,429 dm³ / 9 ≈ 0,159 dm³ und ihre Grundfläche ist 1,268 dm²

Daraus kann man die Pyramidenhöhe ausrechnen.

\(V_{Pyramide} = \frac{1}{3} \cdot Grundfläche \cdot Höhe \)

Comments

Dankeschön, das war sehr hilfreich :)

---

Hey wie bist du auf die 9 ≈ 0,159 dm^3 gekommen und auf die Grundfläche 1,268 dm^2?

Könntest du mir das nochmal erklären?  :)

Lg

---

Wenn der Würfel 90 % des Volumens enthält und die Pyramide 10 %, dann muss man das Würfelvolumen durch 9 dividieren, um auf das Pyramidenvolumen zu kommen.

Die Grundfläche ist ein Quadrat und hat darum den Flächeninhalt Kantenlänge hoch 2.